Вы знаете, что давление газа вызывается тем, что молекулы его бомбардируют стенки сосуда. Позднее, когда мы подойдем к количественному описанию этого явления, нам понадобится знать, с какой скоростью движутся молекулы, ударяясь о стенку, поскольку сила их ударов зависит от скорости. Однако говорить о какой-то определенной скорости молекул совершенно невозможно. В этом случае необходимо использовать вероятностное описание. Молекула может иметь любую скорость, но некоторые скорости предпочтительнее других. Все происходящее в газе можно описать, сказав, что вероятность того, что данная молекула движется с какой-то скоростью между v и v+Δv, будет равна p ( v )Δ v , где р ( v ) — плотность вероятности, которая зависит от скорости v . Позднее я расскажу, как Максвелл, используя общие понятия и идеи теории вероятности, нашел математическое выражение для функции p ( v ) [8] Максвелл получил выражение Cv 2 e - av ^2 , где а — некоторая связанная с температурой постоянная, а С выбирается таким образом, чтобы полная вероятность была равна единице.
. Примерный вид функции p ( v ) показан на фиг. 6.9.
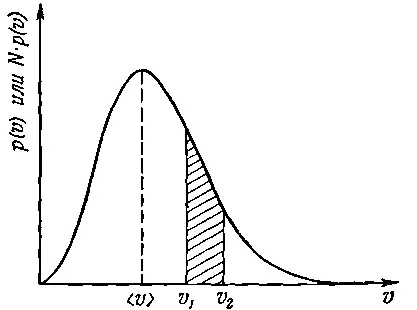
Фиг. 6.9. Распределение молекул газа по скоростям.
Скорость может иметь любую величину, однако больше шансов за то, что она окажется где-то в окрестности наиболее вероятного или ожидаемого значения < v >.
О кривой, показанной на фиг. 6.9, часто говорят в несколько ином смысле. Если мы возьмем газ, заключенный в каком-то сосуде (скажем, объемом 1 л ), то окажется, что в нем имеется огромное количество молекул ( N ≈10 22). Поскольку р ( v )Δv — вероятность того, что первая попавшаяся молекула будет лететь со скоростью, находящейся в интервале Δv, то, по определению, ожидаемое число молекул <���ΔN> со скоростью, находящейся в этом же интервале, будет равно
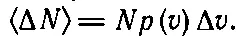 (6.21)
(6.21)
Поэтому Np ( v ) можно назвать «распределением молекул по скоростям». Площадь под кривой между двумя значениями скоростей v 1и v 2[заштрихованная область на фиг. 6.9 для кривой Np ( v )] представляет ожидаемое число молекул со скоростями между v 1и v 2. Но в газе, который содержит обычно огромное число молекул, отклонения от ожидаемого значения будут очень малы (порядка 1/√ N ), поэтому часто мы выбрасываем слово «ожидаемое» и говорим просто: «Число молекул со скоростями между v 1и v 2равно площади заштрихованного участка». Однако нужно все-таки помнить, что речь в таких случаях всегда идет о вероятном числе.
§ 5. Принцип неопределенности
Понятия вероятности оказались очень полезны при описании поведения газа, состоящего из огромного количества молекул. Немыслимо же в самом деле пытаться определить положение и скорость каждой из 10 22молекул! Когда впервые теория вероятности была применена к таким явлениям, то это рассматривалось просто как удобный способ работы в столь сложной обстановке. Однако теперь мы полагаем, что вероятность существенно необходима для описания различных атомных процессов. Согласно квантовой механике, этой математической теории малых частичек, при определении положения частички и ее скорости всегда существует некоторая неопределенность. В лучшем случае мы можем только сказать, что существует какая-то вероятность того, что частица находится вблизи точки х .
Для описания местоположения частицы можно ввести плотность вероятности p 1( x ), так что p 1( x )Δ x будет вероятностью того, что частица находится где-то между х и х +Δx. Если положение частицы установлено достаточно хорошо, то примерный вид функции p 1( x ) может иллюстрировать график, приведенный на фиг. 6.10, а .
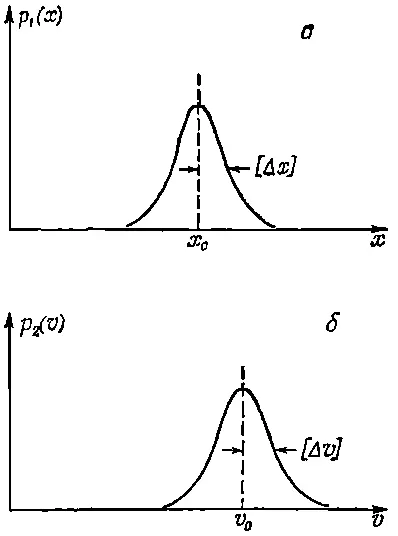
Фиг. 6.10. Плотности вероятности координаты, (а) и скорости (b) частицы.
Точно такое же положение и со скоростью частицы: она тоже неизвестна нам точно. С некоторой вероятностью р 2( v )Δ v частица может двигаться со скоростью, находящейся в интервале между v и v+Δv.
Читать дальше


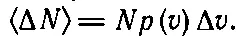 (6.21)
(6.21)





