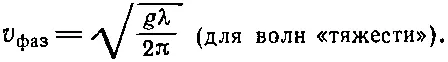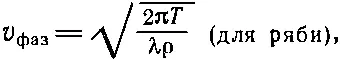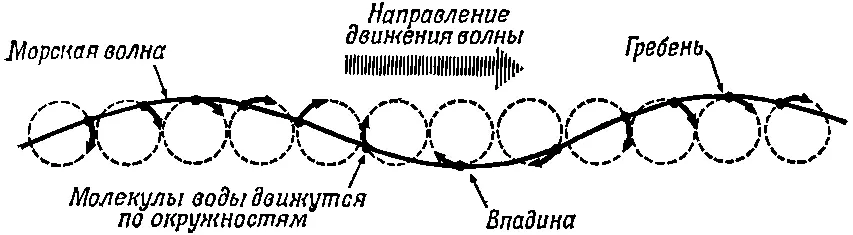
Фиг. 51.9. Волны, на глубокой воде образуются частицами, движущимися по окружности. Обратите внимание на систематический сдвиг фазы от одной окружности к другой. Кок может при этом двигаться плавающий предмет?
Очень интересно определить скорость таких волн. Это должно быть какой-то комбинацией плотности воды, ускорения силы тяжести, которая в данном случае является восстанавливающей силой, и, возможно, длины волны и глубины. Если мы рассмотрим случай бесконечной глубины, то скорость больше не будет зависеть от нее. Но какую бы формулу для фазовой скорости волн мы ни взяли, она должна содержать эти величины в такой комбинации, чтобы давать правильную размерность. Испробовав множество различных способов, мы найдем, что только одна комбинация g и λ может дать нам размерность скорости, именно √( g λ), которая совсем не включает плотности. На самом деле эта формула для фазовой скорости не вполне точна, и полный анализ динамики, в который мы не будем входить, показывает, что все действительно получится так, как у нас, за исключением √(2π), т. е.
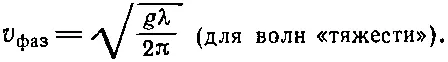
Интересно, что длинные волны бегут быстрее коротких. Так что когда проходящая вдали моторная лодка создает волны, то после некоторого промежутка времени они достигнут берега, но сначала это будут редкие всплески, поскольку первыми приходят длинные волны. Затем приходящие волны становятся все короче и короче, ибо скорость падает как квадратный корень из длины волны.
«Это же неверно,— может возразить кто-нибудь,— ведь чтобы делать такое утверждение, мы должны смотреть на групповую скорость». Правильно, конечно. Формула для фазовой скорости не говорит нам о том, что приходит первым; об этом может нам сказать только групповая скорость. Так что мы должны получить групповую скорость и мы сможем показать, что она равна половине фазовой скорости. Для этого нужно только вспомнить, что фазовая скорость ведет себя как квадратный корень из длины волны. Так же, т. е. как квадратный корень из длины волны, ведет себя и групповая скорость. Но как может групповая скорость быть вдвое меньше фазовой? Посмотрите на группу волн, вызванных проходящей мимо лодкой, и проследите за каким-то определенным гребнем. Вы обнаружите, что он бежит вместе с группой, но постепенно становится все меньше и меньше, а дойдя до переднего фронта, совсем умирает. Но таинственным и непостижимым образом на смену ему с заднего фронта поднимается слабенькая волна и становится она все сильнее и сильнее. Короче говоря, по группе движутся волны, тогда как сама группа движется вдвое медленнее этих волн.
Поскольку групповая и фазовая скорости не равны друг другу, то волны, вызванные движущимся объектом, будут уже не просто коническими, а гораздо более сложными и интересными. Вы можете видеть это на фиг. 51.10, где показаны волны, вызванные движущейся по воде лодкой.

Фиг. 51.10. След прошедшей моторной лодки.
Заметьте, что они совсем не похожи на то, что мы получали для звука (когда скорость не зависит от длины волны), где фронт волны был просто распространяющимся в стороны конусом. Вместо него мы получили волны позади движущегося объекта, фронт которых перпендикулярен его движению, да еще движущиеся под другими углами небольшие волны с боков. Всю эту картину движения волн в целом можно очень красиво воссоздать, зная только, что фазовая скорость пропорциональна квадратному корню из длины волны. Весь фокус заключается в том, что картина волн стационарна относительно лодки (движущейся с постоянной скоростью); все другие виды волн отстанут от нее.
До сих пор мы рассматривали длинные волны, для которых восстанавливающей силой была сила тяжести. Но когда волны становятся очень короткими, то основной восстанавливающей силой оказывается капиллярное притяжение, т. е. энергия поверхностного натяжения. Для волн поверхностного натяжения фазовая скорость равна
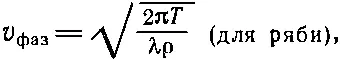
Читать дальше