Ричард Фейнман - Том 1. Механика, излучение и теплота

Между прочим, легко сосчитать полную работу. Полная работа, совершаемая при расширении, равна произведению давления на изменение объема: ∫ PdV . На нашей диаграмме мы откладывали Р вертикально, а V горизонтально. Если обозначать вертикальное расстояние буквой у , а горизонтальное буквой х , то мы получим интеграл ∫ ydx , а это — площадь под кривой. Таким образом, площадь под каждой из пронумерованных кривых измеряет работу, совершенную либо газом, либо нами за соответствующий этап цикла. Легко понять, что чистый выход работы равен площади внутри кривых.

Раз уж мы привели пример одной обратимой машины, то можно предположить, что возможно существование и других таких же устройств. Пусть обратимая машина А забирает Q 1при T 1совершает работу W и возвращает какое-то количество тепла при температуре Т 2. Предположим, что у нас есть еще одна машина В — творение рук человека, уже сконструированная, а может быть, еще и не изобретенная. Можно взять паровую машину, колесо с резиновыми спицами — словом, что угодно. Мы даже не интересуемся, обратима ли эта машина. Важно только, чтобы она забирала тепло Q 1при температуре Т 1и возвращала часть этого тепла при более низкой температуре Т 2. Предположим, что машина В совершает некую работу W'. Теперь покажем, что W ' не может быть больше W ; нет такой машины, которая работала бы лучше, чем обратимая. Но почему? Предположим, что W ' больше W . Тогда мы можем забрать тепло Q 1при температуре Т 1и отдать его машине В . Эта машина совершит работу W ' и отдаст какое-то количество тепла (неважно какое) резервуару с температурой Т 2. После этого мы можем распорядиться какой-то частью работы W ', которую мы считаем больше W . Прибережем пока часть работы W , а остаток W '- W употребим с пользой для себя (фиг. 44.7).

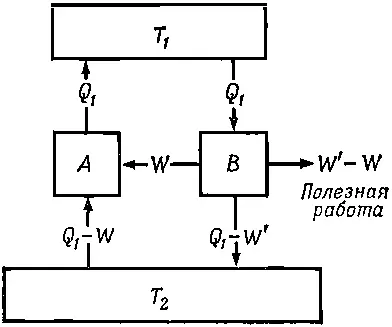
Фиг. 44.7. Машина В заставляет работать обратимую машину А в обратном направлении.

Обладая работой W , можно запустить машину А в обратном направлении, ведь это — обратимая машина . При этом она поглотит какое-то количество тепла из резервуара с температурой Т 2, но зато вернет тепло Q 1резервуару при температуре Т 1. Каков чистый результат этого двойного цикла? Мы вернули все к исходному состоянию и совершили дополнительную работу W '- W . Дело свелось к тому, что мы извлекли энергию из резервуара с температурой Т 2! Тепло Q 1, взятое из резервуара с температурой T 1, было аккуратно возвращено. Раз это тепло все равно возвращается, то в качестве резервуара с температурой Т 1можно взять что-нибудь поменьше океана и заключить это устройство внутрь составной машины А + В . Чистым результатом цикла такой машины будет изъятие из резервуара при температуре Т 2тепла W '- W и превращение его в работу. Но извлечение полезной работы из резервуара при неизменной температуре без других изменений запрещается постулатом Карно. Этого нельзя сделать. Таким образом, не существует таких машин, которые извлекли бы некоторое количество тепла из резервуара при температуре Т 1, возвратили бы какую-то его часть при температуре Т 2и совершили большую работу, чем обратимая машина, работающая при тех же самых температурных условиях.

Предположим теперь, что машина В тоже обратима. Тогда, конечно, не только W ' не больше W , но и W не больше W '. Чтобы доказать это, надо просто обратить предыдущие аргументы. Итак, если обе машины обратимы, то они должны производить одинаковую работу, и мы пришли к блестящему выводу Карно: если машина обратима, то безразлично, как она умудряется превращать тепло в работу. Произведенная машиной работа, если только машина поглощает определенное количество тепла при температуре Т 1и возвращает какую-то его часть при температуре Т 2, не зависит от устройства машины . Так уж устроен мир, и от частных свойств машины это не зависит.

Если бы мы нашли закон, определяющий работу, совершаемую при изъятии тепла Q 1при температуре Т 1и возвращении части этого тепла при температуре T 2, то эта величина была бы универсальной постоянной, не зависящей от свойств вещества. Конечно, если нам известны свойства какого-нибудь вещества, мы можем вычислить интересующую нас величину. После этого мы будем вправе заявить, что все остальные вещества, если с их помощью построить обратимую машину, произведут точно такую же работу. Такова основная идея, ключ, с помощью которого мы можем найти последующие соотношения. Например, мы хотим узнать, насколько резина сжимается при нагревании и насколько она остывает, когда мы позволяем ей сжаться. Предположим, что мы взяли резину в качестве рабочего вещества обратимой машины и совершили обратимый цикл. Чистый результат, полная произведенная работа,— это универсальная функция, великая функция, не зависящая от свойств вещества. Таким образом, мы убеждаемся, что есть нечто, ограничивающее в известном роде разнообразие свойств вещества. Мы не можем сделать эти свойства какими захотим, не можем изобрести вещество, которое, будучи использованным в тепловой машине, произвело бы за обратимый цикл работу больше допустимой. Этот принцип, это ограничение,— единственное реальное правило, которое можно вывести из термодинамики.