Ричард Фейнман - Том 1. Механика, излучение и теплота

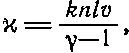(43.42)

при этом (γ-1) kT —средняя энергия молекулы при температуре Т .

Если вспомнить о соотношении nl σ c =1, то теплопроводность можно записать в виде

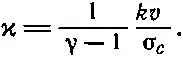(43.43)

Мы получили поистине удивительный результат. Известно, что средняя скорость молекул газа зависит от температуры и не зависит от плотности . Можно думать, что σ с зависит только от размеров молекул. Таким образом, наш очень простой вывод сводится к тому, что теплопроводность ϰ (а следовательно, и скорость потока тепла в каждом частном случае) не зависит от плотности газа! Изменение числа «носителей» энергии при изменениях плотности в точности компенсируется изменением расстояния, которое пробегает «носитель» между столкновениями.

А теперь можно спросить: Действительно ли поток тепла всегда не зависит от плотности газа? Ну а если плотность стремится к нулю и в ящике совсем не остается газа? Конечно, нет! Формула (43.43), как и другие формулы этой главы, выведена в предположении, что средняя длина свободного пробега между столкновениями гораздо меньше любых размеров ящика. Если плотность газа столь мала, что молекула имеет неплохие шансы пробежаться от одной стенки ящика к другой, ни разу не столкнувшись, то все вычисления этой главы рухнут. В этих случаях следует вернуться к кинетической теории и заново все детально рассчитать.

До сих пор мы рассматривали свойства вещества с атомной точки зрения, причем мы пытались, хотя бы в общих чертах, понять, что произойдет, если принять, что вещество состоит из атомов, подчиняющихся тем или иным законам. Однако вещество обладает и такими свойствами, которые можно понять, не изучая подробно его строения. Поисками соотношений между различными свойствами вещества, не углубляясь в изучение внутреннего его строения, занимается термодинамика . Исторически термодинамика стала наукой еще до того, как более или менее точно узнали о внутреннем строении вещества.

Приведем пример: согласно кинетической теории, давление газа вызывается молекулярной бомбардировкой, и нам известно, что при нагревании газа бомбардировка усиливается и давление должно повыситься. И наоборот, если внутрь ящика с газом вдвигается поршень, преодолевающий сопротивление бомбардирующих его молекул, то энергия этих молекул возрастает, а соответственно повышается и температура. Итак, повышая температуру внутри заданного объема, мы увеличиваем давление. Если же мы сжимаем газ, то повышается его температура. Используя кинетическую теорию, можно найти количественные соотношения между этими двумя эффектами, однако каждому понятно, что между давлением и температурой обязательно должна существовать некоторая связь, не зависящая от деталей столкновений.

Рассмотрим еще один пример. Многим, наверное, известно интересное свойство резины — если растянуть ее, она нагреется. Если вы зажмете губами резиновую полоску и, потянув рукой, растянете ее, то отчетливо почувствуете, что она нагрелась. Это нагревание обратимо, т. е. если вы, продолжая держать полоску губами, быстро отпустите ее, то возникнет столь же отчетливое ощущение холода. Это означает, что при растяжении резина нагревается, а при ослаблении натяжения она охлаждается. Наш инстинкт может нам подсказать, что нагретая резина тянет лучше: если растяжение нагревает резину, то нагревание заставит ее сжаться. Действительно, если поднести к растягиваемой грузиком резиновой полоске газовую горелку, то мы заметим, что полоска резко сократится (фиг. 44.1).

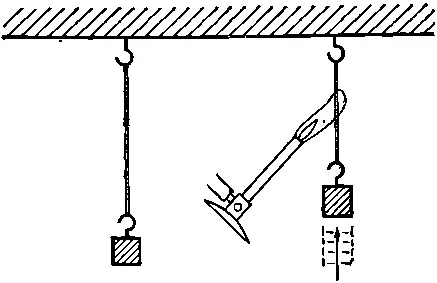
Фиг. 44.1. Нагретая резина.

Таким образом, при нагревании натяжение в резине возрастет, и это вполне согласуется с тем, что при уменьшении натяжения она остывает.

Скрытые в резине механизмы, управляющие этими эффектами, очень сложны. Мы опишем их с молекулярной точки зрения, хотя главная задача этой главы — научиться понимать связь между такими эффектами независимо от молекулярной модели. Тем не менее, именно исходя из молекулярной модели, мы можем показать, что оба эти явления тесно связаны. Поведение резины можно объяснить так. Представьте себе, что резина, по существу, огромный клубок, состоящий из очень длинных молекул, что-то вроде «молекулярных макарон», но с небольшим дополнительным усложнением: между этими молекулярными цепочками имеются соединительные цепочки. Таким образом, моделью куска резины могут служить слипшиеся во время варки макароны, образующие огромный ком. Когда мы растягиваем такой клубок, некоторые молекулярные цепи стремятся вытянуться в линию вдоль направления растяжения. В то же время все цепи участвуют в тепловом движении и непрерывно сталкиваются друг с другом. Поэтому такая цепь, когда ее растягивают, не остается в натянутом виде, так как об нее ударяют со всех сторон другие цепи и другие молекулы, и она будет вынуждена запутаться снова. Поэтому истинная причина того, почему резина все время стремится сократиться, заключается в следующем: при растяжении цепи действительно вытягиваются вдоль одной линии, но тепловые движения цепей стремятся запутать их снова и сократить их длину. Поэтому если растянуть цепи и увеличить температуру, то усилится и бомбардировка цепей, что приведет к увеличению натяжения. Этим объясняется способность нагретой резины поднять более тяжелый груз. Если растянутую в течение некоторого времени резину отпустить, то каждая цепь становится мягче, ударяющиеся о расслабленные цепи молекулы теряют энергию, и температура падает.