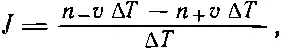 (43.21)
(43.21)
или
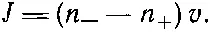 (43.22)
(43.22)
А что понимать под n -и n +? Когда мы говорим «плотность слева от площадки», то как далеко налево? Мы должны измерить плотность в том месте, откуда молекула отправляется в свой «свободный полет», потому что число стартующих молекул определяется числом молекул, находящихся в этом месте. Таким образом, n -— это плотность молекул на расстоянии длины свободного пробега l слева от нашей воображаемой площадки, а n +— плотность молекул на расстоянии длины свободного пробега справа от нее.
Распределение особых молекул в ящике удобно описывать с помощью непрерывной функции x, y и z , которую мы обозначим n a. Под n a( x, y, z ) нужно понимать плотность особых молекул в маленьком объеме вокруг точки ( x, y, z ). Тогда разность ( n +- n -) можно представить в виде
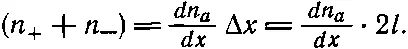 (43.23)
(43.23)
Подставляя этот результат в (43.22) и пренебрегая множителем 2, получаем
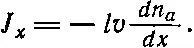 (43.24)
(43.24)
Мы выяснили, что поток особых молекул пропорционален производной плотности, или, как иногда говорят, «градиенту плотности».
Ясно, что мы сделали несколько грубых приближений. Не говоря уже о том, что мы постоянно забывали о множителях, мы использовали v , когда нужно было ставить v x , а разместив объемы, содержащие молекулы n +и n -, на концах перпендикуляров к площадке, взяли перпендикуляры длиной l . Между тем для тех молекул, которые движутся не перпендикулярно к поверхности, l соответствует длине наклонного пути. Можно исправить эти недоделки; более тщательный анализ показал бы, что правую часть уравнения (43.24) нужно умножить на 1/ 3. Итак, более правильный ответ выглядит следующим образом:
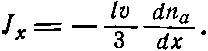 (43.25)
(43.25)
Аналогичные уравнения можно написать для токов вдоль y - и z-направлений.
С помощью макроскопических наблюдений можно измерить ток J x и градиент плотности dn a / dx . Их отношение, найденное экспериментально, называется «коэффициентом диффузии» D . Это значит, что
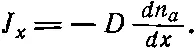 (43.26)
(43.26)
Мы смогли показать, что ожидаемое значение коэффициента D для газа равно
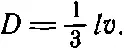 (43.27)
(43.27)
Пока мы изучили в этой главе два разных процесса: подвижность (дрейф молекул под действием «внешней» силы) и диффузию (разбегание молекул, определяемое только внутренними силами, случайными столкновениями). Однако эти процессы связаны друг с другом, потому что в основе обоих явлений лежит тепловое движение, и оба раза в расчетах появлялась длина свободного пробега l .
Если в уравнение (43.25) подставить l = v τ и τ=μm, то получится
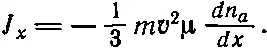 (43.28)
(43.28)
Ho mv 2зависит только от температуры. Мы еще помним, что
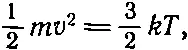 (43.29)
(43.29)
так что
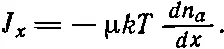 (43.30)
(43.30)
Таким образом, D , коэффициент диффузии , равен произведению kT на μ, коэффициент подвижности :
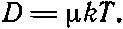 (43.31)
(43.31)
Оказывается, что (43.31) — это точное соотношение между коэффициентами. Хотя мы исходили из очень грубых предположений, не нужно к нему добавлять никаких дополнительных множителей. Можно показать, что (43.31) в самом деле всегда удовлетворяется точно. Это верно даже в очень сложных случаях (например, для случая взвешенных в жидкости мелких частиц), когда наши простые вычисления явно отказываются служить.
Читать дальше

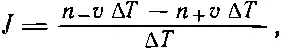 (43.21)
(43.21)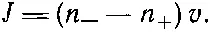 (43.22)
(43.22)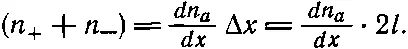 (43.23)
(43.23)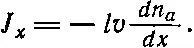 (43.24)
(43.24)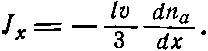 (43.25)
(43.25)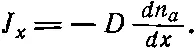 (43.26)
(43.26)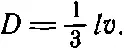 (43.27)
(43.27)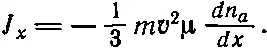 (43.28)
(43.28)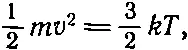 (43.29)
(43.29)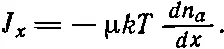 (43.30)
(43.30)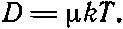 (43.31)
(43.31)




