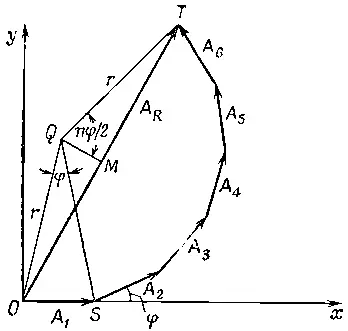
Фиг. 30.1. Результирующая амплитуда шести аквидистантных источников при разности фаз φ между каждыми двумя соседними источниками.
Вершины многоугольника лежат, конечно, на окружности, и чтобы легче было определить результирующую амплитуду, найдем радиус этой окружности. Пусть Q есть ее центр. Тогда угол OQS равен как раз фазе φ (поскольку радиус QS образует с А 2такой же угол, как QO с A 1). Следовательно, радиус r должен удовлетворять равенству А =2 r sinφ/2, откуда мы и находим величину r. Далее, большой угол OQT равен nφ; следовательно, A R=2 r sinnφ/2. Исключая из обоих равенств r, получаем
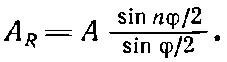 (30.2)
(30.2)
Таким образом, суммарная интенсивность оказывается равной
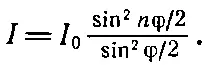 (30.3)
(30.3)
Проанализируем это выражение и обсудим вытекающие из него следствия. Прежде всего, положив n=1, получим, как и следовало ожидать, I=I 0. Проверим формулу для n=2: с помощью соотношения sinφ=2sin φ/2cosφ/2 сразу находим А R =2 Acos φ/2, что совпадает с (29.12).
Мы вынуждены рассматривать сложение полей от многих источников потому, что в этом случае интенсивность в одном направлении получается много больше, чем в соседних, т. е. все побочные максимумы интенсивности оказываются гораздо меньше основного. Чтобы понять этот факт, начертим кривую соответствующую выражению (30.3) для больших n и φ, близких к нулю. Прежде всего, когда φ точно равно нулю, мы получаем отношение 0/0, но фактически для бесконечно малых φ отношение синусов равно n 2, так как синус можно заменить его аргументом. Таким образом, максимум кривой в n 2раз больше интенсивности одного осциллятора. Этот результат легко понять, поскольку при нулевой разности фаз все n маленьких векторов складываются в один вектор, в n раз больший исходного, а интенсивность увеличивается в n 2раз.
С ростом фазы φ отношение двух синусов падает и обращается в нуль в первый раз при nφ/2=π, поскольку sinπ=0. Другими словами, значение φ=2π/ n отвечает первому минимуму кривой (фиг. 30.2). С точки зрения векторов на фиг. 30.1 первый минимум возникает в том случае, когда стрелки векторов возвращаются в исходную точку, при этом полная разность фаз от первого до последнего осциллятора равна 2π.
Перейдем к следующему максимуму и покажем, что он действительно, как мы и ждали, много меньше первого. Для точного определения положения максимума необходимо учитывать, что и числитель, и знаменатель в (30.3) оба меняются с изменением φ. Мы не станем этого делать, поскольку при большом n sinφ/2 меняется медленнее sinφ/2 и условие sinφ/2=1 дает положение максимума с большой точностью. Максимум sin 2nφ/2 достигается при nφ/2=Зπ/2 или φ=Зπ/n. Это означает, что стрелки векторов описывают полторы окружности.
Подставляя φ=3π/n, получаем sin 23π/2=1 в числителе (30.3) (с этой целью и был выбран угол φ) и sin 23n/2n в знаменателе. Для достаточно большого n можно заменить синус его аргументом: sin 3π/2n=3π/2n. Отсюда интенсивность во втором максимуме оказывается равной I=I 0(4n 2/9π 2). Но n 2I 0— не что иное, как интенсивность в первом максимуме, т. е. интенсивность второго максимума получается равной 4/9π 2от максимальной, что составляет 0,047, или меньше 5%! Остальные максимумы, очевидно, будут еще меньше. Таким образом, возникает очень узкий основной максимум и очень слабые дополнительные максимумы по обе стороны от основного.
Можно показать, что площадь под кривой интенсивности, включая все максимумы, равна 2πnI 0и в два раза превышает площадь пунктирного прямоугольника на фиг. 30.2.
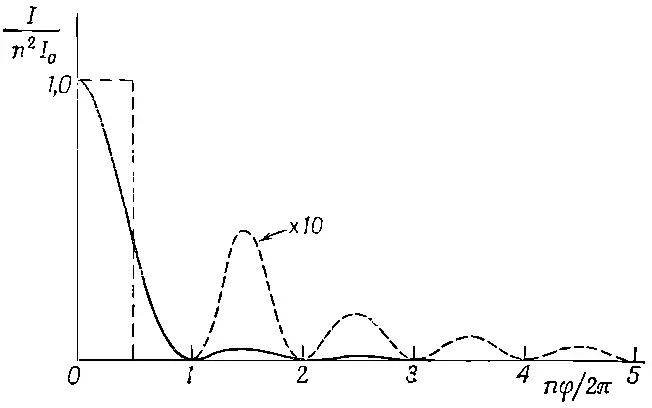
Фиг. 30.2. Зависимость интенсивности от фазового угла для большого числа осцилляторов с одинаковыми амплитудами.
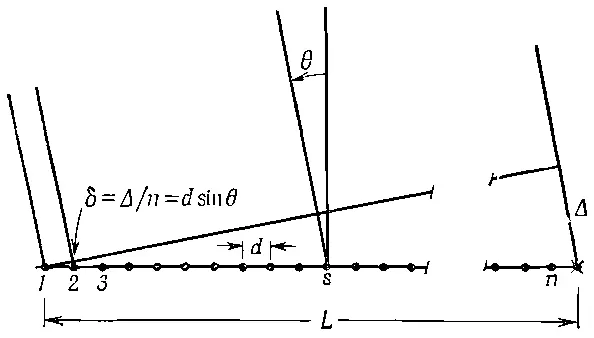
Посмотрим теперь, что дает формула (30.3) в приложении к разным случаям. Пусть источники расположены на одной линии, как показано на фиг. 30.3.
Читать дальше


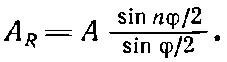 (30.2)
(30.2)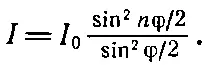 (30.3)
(30.3)






