Мы уже знаем, как надо складывать и умножать комплексные числа; сумма двух комплексных чисел ( р + iq )+( r + is ) — это число (p+r)+i(q+s). Но вот возведение комплексных чисел в комплексную степень — уже задача потруднее. Однако она оказывается не труднее задачи о возведении в комплексную степень действительных чисел. Посмотрим поэтому, как возводится в комплексную степень число 10, не в иррациональную, а комплексную; нам надо знать число 10 (r+is). Правила (22.1) и (22.2) несколько упрощают задачу
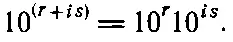 (22.5)
(22.5)
Мы знаем, как вычислить 10 r, перемножить числа мы тоже умеем, не умеем только вычислить 10 is. Предположим, что это комплексное число x + iy . Задача: дано s , найти х и у . Если
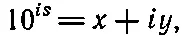
то должно быть верным и комплексно сопряженное уравнение
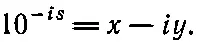
(Некоторые вещи можно получить и без вычислений, надо просто использовать правила.) Перемножая эти равенства, можно получить еще один интересный результат
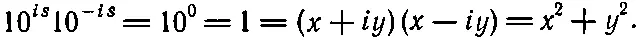 (22.6)
(22.6)
Если мы каким-то образом найдем х , то определить у будет очень легко.
Однако как все-таки возвести 10 в мнимую степень? Где искать помощи? Правила нам уже не помогут, но утешает вот что: если удастся возвести 10 в какую-нибудь одну мнимую степень, то ничего не стоит возвести 10 уже в любую степень. Если известно 10 isдля одного значения s , то вычисление в случае вдвое большего s сводится к возведению в квадрат и т. д. Но как же возвести 10 в хотя бы одну мнимую степень? Для этого сделаем дополнительное предположение; его, конечно, нельзя ставить в один ряд с правилами (22.1) и (22.2), но оно приведет к разумным результатам и позволит нам шагнуть далеко вперед. Предположим, что «закон» 10 ε=1+2,3025ε (когда ε очень мало) верен не только для действительных, но и для комплексных ε. Если это так, то 10 is=1+2,3025·is при s→0. Предполагая, что s очень мало (скажем, равно 1/1024), мы получаем хорошее приближение числа 10 is.
Теперь можно составить таблицу, которая позволит вычислить все мнимые степени 10, т. е. найти числа x и y. Надо поступить так. Начнем с показателя 1/1024, который мы считаем равным примерно 1+2,3025 i/1024. Тогда
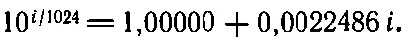 (22.7)
(22.7)
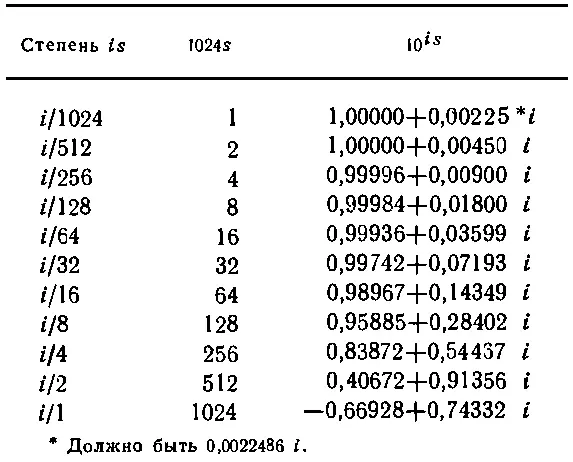
Умножая это число само на себя много раз, мы дойдем до степеней более высоких. Мы просто-напросто перевернули процедуру составления таблицы логарифмов и, вычислив квадрат, 4-ю степень, 8-ю степень и т. д. числа (22.7), составили табл. 22.3. Интересно, что сначала все числа х были положительными, а потом вдруг появилось отрицательное число. Это значит, что существует число s, для которого действительная часть 10 isравна нулю . Значение iу в этом случае равно i , т. е. 10 is=i, или is=log 10i. В качестве примера (см. табл. 22..3) вычислим с ее помощью log 10i. Процедура поиска log 10i в точности повторяет то, что мы делали, вычисляя log 102.
Произведение каких чисел из табл. 22.3 равно чисто мнимому числу? После нескольких проб и ошибок мы найдем, что лучше всего умножить «512» на «128». Их произведение равно 0,13056+0,99144i. Приглядевшись к правилу умножения комплексных чисел, можно понять, что надежду на успех сулит умножение этого числа на число, мнимая часть которого приблизительно равна действительной части нашего числа. Мнимая часть «64» равна 0,14349, что довольно близко к 0,13056. Произведение этих чисел равно -0,01350+0,99993i. Мы перескочили через нуль, поэтому результат нужно разделить на 0,99996+0,00900 i. Как это сделать? Изменим знак i и умножим на 0,99996-0,00900 i (ведь x 2+y 2=1). В конце концов обнаружим, что если возвести 10 в степень i(1/1024) (512+128+64-4-2+0,20) или 698,20i/1024, то получится мнимая единица. Таким образом, log 10i=0,068226 i .
Таблица 22.3. последовательное: вычисление квадратов 10 i/1024=1+0,0022486i
Читать дальше

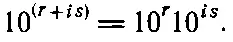 (22.5)
(22.5)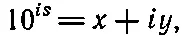
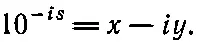
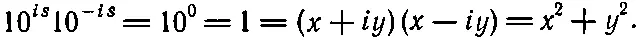 (22.6)
(22.6)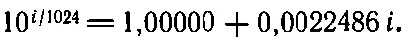 (22.7)
(22.7)





