Хотя вычисление собранных в таблицы значений — процедура чисто техническая, а все же дело это интересное и имеет большую историю. Поэтому посмотрим, как это делается. Мы вычислим не только x=10 √2, но решим и другую задачу: 10 x=2, или x=log 102. При решении этих задач мы не откроем новых чисел; это просто вычислительные задачи. Решением будут иррациональные числа, бесконечные десятичные дроби, а их как-то неудобно объявлять новым видом чисел.
Подумаем, как решить наши уравнения. Общая идея очень проста. Если вычислить 10 1и 10 1/10, и 10 1/100, и 10 1/1000, и т. д., а затем перемножить результаты, то мы получим 10 1,414..., или 10 √2. Поступая так, мы решим любую задачу такого рода. Однако вместо 10 1/10и т. д. мы будем вычислять 10 1/2, 10 1/4и т. д. Прежде чем начинать вычисления, объясним еще, почему мы обращаемся к числу 10 чаще, чем к другим числам. Мы знаем, что значение таблиц логарифмов выходит далеко за рамки математической задачи вычисления корней, потому что
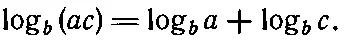 (22.3)
(22.3)
Это хорошо известно всем, кто пользовался таблицей логарифмов, чтобы перемножить числа. По какому же основанию b брать логарифмы? Это безразлично; ведь в основу таких вычислений положен только принцип, общее свойство логарифмической функции. Вычислив логарифмы один раз по какому-нибудь произвольному основанию, можно перейти к логарифмам по другому основанию при помощи умножения. Если умножить уравнение (22.3) на 61, то оно останется верным, поэтому если перемножить все числа в таблице логарифмов по основанию b на 61, то можно будет пользоваться и такой таблицей. Предположим, что нам известны логарифмы всех чисел по основанию b. Иначе говоря, можно решить уравнение b а = с для любого с; для этого существует таблица. Задача состоит в том, как найти логарифм этого же числа с по другому основанию, например х . Нам нужно решить уравнение х а '= с . Это легко сделать, потому что х всегда можно представить так: x = b t . Найти t , зная х и b, просто: t = log b x . Подставим теперь х = b t в уравнение x a '= с ; оно перейдет в такое уравнение: (b t) а'=b ta'=с. Иными словами, произведение ta ' есть логарифм с по основанию b. Значит, a '= a / t . Таким образом, логарифмы по основанию х равны произведениям логарифмов по основанию b на постоянное число 1/ t . Следовательно, все таблицы логарифмов эквивалентны с точностью до умножения на число 1/ log b x . Это позволяет нам выбрать для составления таблиц любое основание, но мы решили, что удобнее всего взять за основание число 10. (Может возникнуть вопрос: не существует ли все-таки какого-нибудь естественного основания, при котором все выглядит как-то проще? Мы попытаемся ответить на этот вопрос позднее. Пока все логарифмы будут вычисляться по основанию 10.)
Теперь посмотрим, как составляют таблицу логарифмов. Работа начинается с последовательных извлечений квадратного корня из 10. Результат можно увидеть в табл. 22.1.
Таблица 22.1 последовательные извлечения КВАДРАТНОГО КОРНЯ ИЗ 10
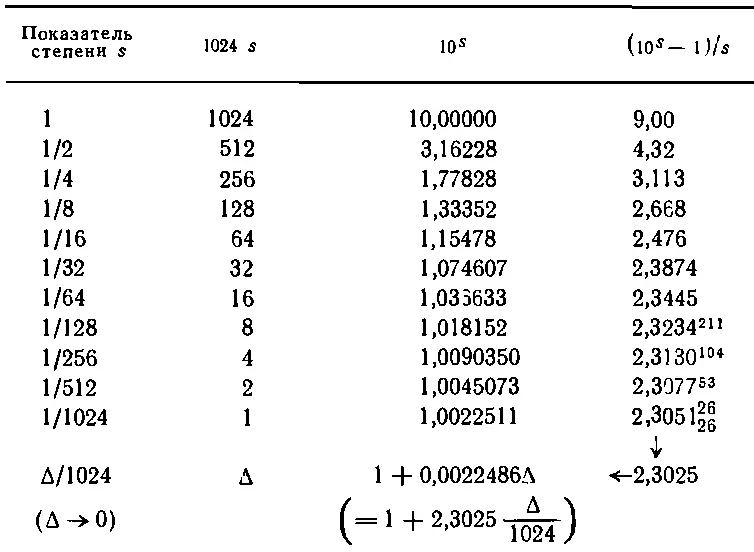
Показатели степеней записаны в ее первом столбце, а числа 10 S— в третьем. Ясно, что 10 1=10. Возвести 10 в половинную степень легко — это квадратный корень из 10, а как извлекать квадратный корень из любого числа, знает каждый [16] Квадратный корень лучше всего извлекать не тем способом, которому обычно учат в школе, а немного иначе. Чтобы извлечь квадратный корень из числа N, выберем достаточно близкое к ответу число а, вычислим N/a и среднее а'= 1 / 2 [a+(N/а)]; это среднее будет новым числом а, новым приближением корня из N. Этот процесс очень быстро приводит к цели: число значащих цифр удваивается после каждого шага.
. Итак, мы нашли первый квадратный корень; он равен 3,16228. Что это дает? Кое-что дает. Мы уже можем сказать, чему равно 10 0,5, и знаем по крайней мере один логарифм. Логарифм числа 3,16228 очень близок к 0,50000. Однако нужно еще приложить небольшие усилия: нам нужна более подробная таблица. Извлечем еще один квадратный корень и найдем 10 1/4,что равно 1,77828. Теперь мы знаем еще один логарифм: 1,250— это логарифм числа 17,78; кроме того, мы можем сказать, чему равно 10 0,75: ведь это 10 (0,5+0,25), т. е. произведение второго и третьего чисел из третьего столбца табл. 22.1. Если сделать первый столбец таблицы достаточно длинным, то таблица будет содержать почти все числа; перемножая числа из третьего столбца, мы получаем 10 почти в любой степени. Такова основная идея таблиц. В нашей таблице содержится десять последовательных корней из 10; основной труд по составлению таблицы вложен в вычисления этих корней.
Читать дальше

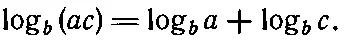 (22.3)
(22.3)





