Александр Львовский - Отличная квантовая механика

Интересно отметить, что термина «фотон» в то время не существовало. Его ввел в 1926 г. специалист по физической химии Гильберт Льюис [13] G. N. Lewis, The conservation of photons , Nature 118 , 874 (1926). .

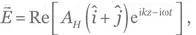Например, если A H= A Vи ϕ H= ϕ V= 0, то соответствующая классическая волна выглядит как т. е. линейно поляризована под углом +45°. Соответственно, состояние 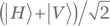(где делитель 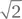связан с нормированием) обозначает единичный фотон с линейной поляризацией под +45°. В табл. 1.1 вы можете увидеть еще несколько примеров [14] Обсуждение договоренностей, принятых для состояний с круговой (циркулярной), поляризацией, см. в сноске 141. .

Из этого следует, что состояния | H ⟩ и | V ⟩ образуют в гильбертовом пространстве поляризационных состояний фотона ортонормальный базис — т. е. пространство двумерно. Действительно, прежде всего эти состояния ортогональны и потому линейно независимы (упр. A.17). Кроме того, любая поляризованная классическая волна может быть записана в виде (1.1), так что любое поляризационное состояние фотона тоже может быть записано аналогично (1.2), т. е. как линейная комбинация состояний | H ⟩ и | V ⟩. Мы будем называть базис {| H ⟩,| V ⟩} каноническим базисом нашего гильбертова пространства.

Упражнение 1.3.Покажите, что:

a) поляризационные состояния ±45° образуют ортонормальный базис;

b) правое и левое круговые поляризационные состояния образуют ортонормальный базис.

Упражнение 1.4.Разложите | H ⟩ и | V ⟩ по базисам {|+⟩,|—⟩} и {| R ⟩,| L ⟩}.

Упражнение 1.5.Разложите | a ⟩ = |+30°⟩ и | b ⟩ = |–30°⟩ по базисам {| H ⟩,| V ⟩}, {|+⟩,|—⟩} и {| R ⟩,| L ⟩}. Найдите скалярное произведение ⟨a|b⟩ во всех трех базисах, используя операцию перемножения матриц. Одинаковые ли получились результаты?

Здесь есть сложный момент, который следует прояснить. Множество углов поляризации линейно поляризованных фотонов — континуум. Но в случае одномерного движения частицы, о котором говорилось в предыдущем разделе, множество позиционных состояний — также континуум. Почему же мы говорим, что одно из этих гильбертовых пространств имеет размерность два, а другое — бесконечность?

Разница в том, что линейно поляризованные состояния могут быть записаны в виде (1.2), т. е. в виде суперпозиции других линейно поляризованных состояний. Если мы поместим поляризующий светоделитель (разд. В.2), пропускающий только горизонтально поляризованные фотоны, на пути диагонально поляризованной волны, часть ее пройдет сквозь светоделитель. Это означает, что диагонально поляризованный фотон может быть обнаружен в горизонтальном поляризационном состоянии.

Состояния же, связанные с разными положениями в пространстве, напротив, все ортогональны: частицу, приготовленную в состоянии | x = 3 м⟩, невозможно обнаружить в точке x = 4 м. Также невозможно записать позиционное состояние в виде суперпозиции других позиционных состояний. Это значит, что соответствующее гильбертово пространство должно иметь намного более широкий базис, чем гильбертово пространство поляризационных состояний.

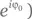Для классической волны (1.1) сдвиг фаз одновременно горизонтального и вертикального компонентов на равную величину (т. е. ϕ H→ ϕ H+ ϕ 0, ϕ V→ ϕ V+ ϕ 0, что эквивалентно умножению правой части на не меняет ее поляризации.

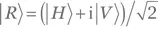Аналогичное правило применимо и к квантовым состояниям. Умножение вектора состояния на eiϕ не меняет физической природы состояния. К примеру, | V ⟩, i| V ⟩ и —| V ⟩ представляют один и тот же физический объект, как и, скажем, и 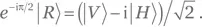По этой причине мы на время пренебрежем множителем e−iωt в (1.2).

Мы называем комплексную величину eiϕ с действительным ϕ фазовым множителем . Умножение квантового состояния на фазовый множитель называется применением фазового сдвига на ϕ. Соответственно мы говорим, что применение фазового сдвига к квантовому состоянию не меняет его физических свойств. Как мы увидим в следующем разделе, это правило оказывается весьма общим: оно выполняется для всех физических систем, не только для электромагнитных волн. Разумеется, фазовый сдвиг должен быть глобальной природы (overall phase shift): если мы применим его только к части состояния, это состояние изменится. 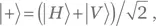Например, если мы применим фазовый сдвиг на π/2 к вертикальному компоненту поляризованного под +45° фотона, то получим 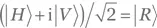— фотон с правой круговой поляризацией, т. е. физически отличный от первоначального объекта.