Julian Barbour - The End of Time - The Next Revolution in Physics

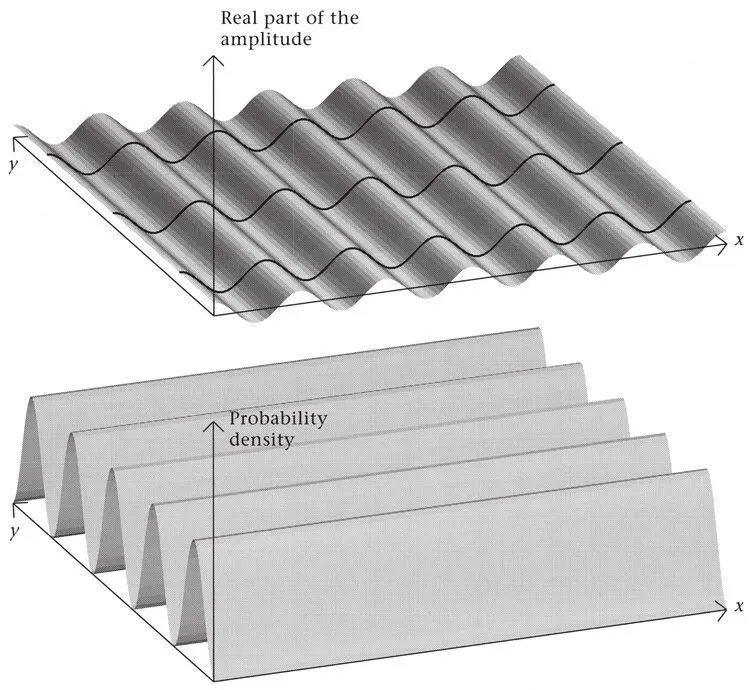
Figure 47.If two inclined but otherwise identical plane waves like the one at the top are added, the figure at the bottom is obtained. The ridges run along the direction of the light rays’ in the original plane waves. (The top figure shows the amplitude, the bottom the square of the added waves, since in quantum mechanics that measures the probability density.)

Figure 48 brings to mind a passage in A Midsummer Night’s Dream that has haunted poets for centures:

And, as imagination bodies forth

The forms of things unknown, the poet’s pen

Turns them to shapes, and gives to airy nothing

A local habitation, and a name.

The intersection of two wave fields does not result in any distinguished point, just a field of parallel ridges. There is no ‘local habitation’. But if the crests of three or more waves intersect at a common point – so that the waves are in phase there – and their amplitudes are varied appropriately, then a point becomes distinguished. A localized ‘blob’ is formed. As Schrödinger realized with growing excitement in the winter of 1925/6, this begins to look like a particle.

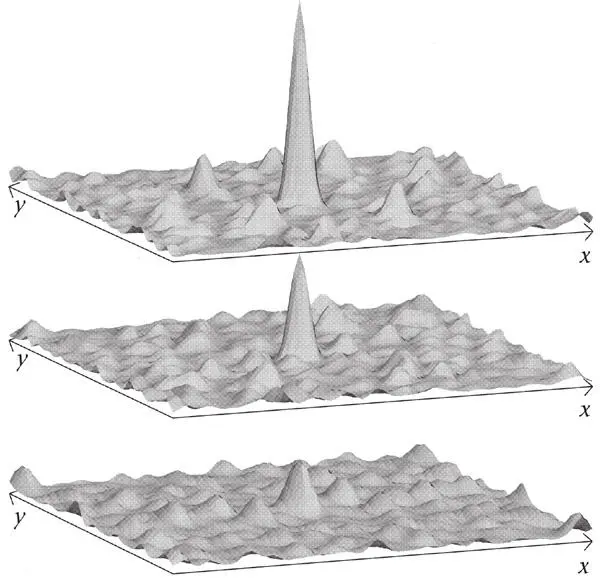
Figure 48.These wave patterns are obtained (from the bottom upward) by adding increasing numbers of plane waves oriented within a small range of directions. All waves have a crest where the ‘spike’ rises from the ‘choppy’ pattern. Their amplitudes also vary in a range, since otherwise ‘ridges’ like those in Figure 47 are obtained.

The pièce de résistance is finally achieved if the waves of different wavelengths move and do so with different speeds. This often happens in nature. In most media – above all in vacuum – light waves all propagate with the same speed. However, in some media the waves of different wavelengths travel at different speeds. Since waves of different wavelengths have different colours, this can give rise to beautiful chromatic effects. In quantum mechanics, the waves associated with ordinary matter particles like electrons, protons and neutrons always propagate at different speeds, depending on their wavelengths. The relationship between the wavelength and the speed of propagation is called their dispersion relation .

Figure 49 has been constructed using such a dispersion relation. The initial ‘spike’ (wave packet) at the bottom is the superposition of waves of different angles in a small range of wavelengths. The dispersion relation makes each wave in the superposition move at a different speed. At the initial time, the waves are all in phase at the position of the ‘spike’, but the position at which all the waves are in phase moves as the waves move. The ‘spike’ moves! Its positions are shown at three times (earliest at the bottom, last at the top). This wave packet disperses quite rapidly because relatively few waves have been used in its construction. In theoretical quantum mechanics, one often constructs so-called Gaussian wave packets, which contain infinitely many waves all perfectly matched to produce a concentrated wave packet. These persist for longer.

It is a remarkable fact about waves in general and quantum mechanics in particular that the wave packet moves with a definite speed, which is known as the group velocity and is determined by the dispersion law. It is quite different from the velocities of any of the individual waves that form the packet. Only when there is no dispersion and all the waves travel at the same speed is the velocity of the packet the same as the speed of propagation of the waves. These remarkable purely mathematical facts about superposition of waves were well known to Schrödinger at the time he made his great discoveries – one of which was that this beautiful mathematics seemed to be manifested in nature.

This led him to propose the wave-packet interpretation of quantum mechanics. His main concern was to show how a theory based on waves could nevertheless create particle-like formations. A potential strength of his proposal was that particle-like behaviour could be expected only above a certain scale. Over short enough distances, within atoms or in colliding wave packets, the full wave theory would have to be used, but in many circumstances it seemed that particles should be present. With total clarity, which shines through his marvellous second paper on wave mechanics, he saw that if particles are associated with waves, then in atomic physics we must expect an exact parallel with geometrical optics. There will be many circumstances in which ordinary Newtonian particles seem to be present, but in the interior of atoms, for example, where the potential changes rapidly, we shall have to use the full wave theory. Schrödinger’s second paper contains wonderful insights.

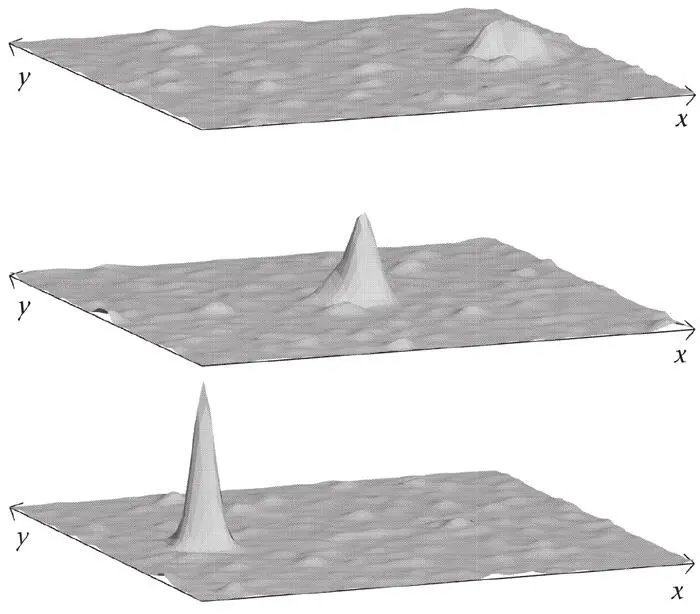
Figure 49.A moving wave packet obtained by adding plane waves having slightly different orientations, wavelengths and propagation velocities. The initially sharply peaked packet disperses quite quickly, as shown in the two upper figures.

Unfortunately, his idea soon ran into difficulties. He had been aware of one from the start. For a single particle, the configuration space is ordinary space, and the idea that the wave function represents charge density makes sense. But he was well aware that his wave function was really defined for a system of particles and therefore had a different value for each configuration of them. I highlighted this earlier by imagining ‘wave-function meters’ in a room which showed the effect of moving individual atoms in models of molecules. It is difficult to see how the wave function can be associated with the charge density of a single particle in space.

Another problem actually killed the proposal. Although wave packets do travel as if they were a particle, they do spread. This was the one effect that Schrödinger failed to grasp initially. He actually did detailed and beautiful calculations for one special case – the two-dimensional harmonic oscillator, or conical pendulum. If a lead bob suspended on a weightless thread is pulled to one side and released, it will swing backwards and forwards like an ordinary pendulum. However, if it is given a sidewise jolt as well it will trace out an ellipse.

Schrödinger was able to show that for the quantum states corresponding to large ellipses it is possible to form wave packets that do not spread at all – the wave packets track round the ellipse for ever. This was a truly lovely piece of work, but misleading. Murphy’s law tripped up Schrödinger. The harmonic oscillator is exceptional and is essentially the only system for which wave packets hold together indefinitely. In all other cases they spread, doing so rapidly for atomic particles. This doomed the idea of explaining particle-like behaviour by the persistence of wave packets, as Heisenberg noted with some satisfaction. (Most of the founding fathers of quantum mechanics defended their own particular directions with great fervour. Schrödinger hated quantum jumps, and found the extreme abstraction of Heisenberg’s matrix mechanics ‘positively repulsive’.)

However, the notion of a wave packet is beautiful and transparent, and has been widely and effectively used. This has tended to make people think that Schrödinger’s original idea was still to a large degree right, and does explain why classical particle-like behaviour (restricted in its accuracy only by the Heisenberg uncertainty relation) is so often observed, especially in macroscopic bodies. There is one great difficulty, though. We can construct wave packets with strongly expressed particle-like properties, but we have to superimpose many different semiclassical solutions in just the right way. There must be a relatively small range of directions and wavelengths, adjustment of the wave amplitudes and, above all, coincidence of the phases of all waves at one point. Nothing in the formalism of quantum mechanics explains how this miraculous pre-established harmony should occur in nature. A single semiclassical solution might well arise spontaneously and naturally. But that will be associated with a whole family of classical trajectories, which exist only as formal constructions – they are at best latent histories. Quantum mechanics generally gives a wave function spread out in a uniform regular manner. Even if by some miracle we could ‘manufacture’ some wave packet, it would inevitably spread. Some further decisive idea is needed to explain how a universe described by quantum mechanics appears so classical and unique.