Julian Barbour - The End of Time - The Next Revolution in Physics

The italics are mine. Lanczos’s account does end with Schrödinger’s discoveries, but I think it can be taken one step further. By the way, do not worry about the call for ‘concentrated thinking’. If you have got this far, you will not fail now.

Hamilton made several separate discoveries, but the most fundamental result is simple and easy to visualize. Two characteristic situations are encountered in wave theory – ‘choppy’ waves, as on a squally sea, and regular wave patterns. Hamilton was studying the connection between Kepler’s early theory of light rays and the more modern wave theory introduced by Young and Fresnel. Hamilton assumed that light passing through lenses took the form of very regular, almost plane waves of one frequency (Figure 45).

In optics, many phenomena can be explained by such waves. To do this, we need to know how the wave crests are bent and how the wave intensity, which is measured by the square of the wave amplitude (Figure 45), varies. In general, when the wave is not very regular, the ways in which the wave crests bend and the amplitude varies are interconnected, and it is not possible to separate their behaviour. However, as the behaviour gets more regular, the amplitude changes less and simultaneously ceases to affect the bending of the wave crests. Hamilton found the equation that governs the disposition of the wave crests in this case. Now known as the eikonal equation , it is the foundation of all optical instruments – microscopes, telescopes – and also electron microscopes. Indeed, numerous effects in optics are fully explained by the bending of the wave crests. However, other phenomena, above all the diffraction and spreading of light when it passes through a small orifice, can be explained only by the full wave theory. In these phenomena the regular pattern of wave crests is broken up.

Figure 45.An example of a regular wave pattern, showing wave crests and the lines that run at right angles to them. Such patterns are characterized by two independent quantities – the wavelength and the amplitude (the maximum height of the wave).

We shall stick to phenomena in which the wave crests remain regular. Lines that run at right angles to such wave crests can be defined; they are easy to visualize (Figure 45). Hamilton’s work in the 1820s showed that these lines correspond to the older idea of light rays, and that there are two seemingly quite different ways of explaining the behaviour of light and the functioning of optical instruments. In the older, more primitive way, light is composed of tiny particles (corpuscles) that travel along straight lines in empty space, but are bent in air, water and optical instruments (made of glass). The theory of light corpuscles works because the paths they take, along Kepler’s light rays, coincide with the lines that run at right angles to the wave crests. This is the second of Hamilton’s great discoveries: if light is a wave phenomenon, there are nevertheless many occasions in which it can be conceived as tiny particles that travel along these rays.

This insight led to the distinction between wave optics and geometrical optics , which uses light rays. Innumerable experiments show that only wave optics, in which light is described by waves, can explain certain phenomena. The earlier theory of light rays simply fails under these circumstances. Equally, there are many cases in which geometrical optics, with its Keplerian light rays, functions perfectly well. We see here the typical situation that arises when a new theory supplants an old one. The new theory invariably uses very different concepts – it ‘inhabits a different world’ – yet it can explain why the old theory worked as well as it did and why it is that it fails where it does. Where the wave pattern becomes irregular, geometrical optics ceases to be valid.

Geometrical optics shows how theories that explain many phenomena impressively and simply can still give a misleading picture. As my daughter learned on those frosty nights, this had happened in ancient astronomy. Ptolemy’s epicycles gave a beautifully simple and successful theory of planetary motion, but were made redundant when Copernicus made the Earth mobile. Geometrical optics is another classic example of a ‘right yet wrong’ theory. In fact, with its confrontation and reconciliation of seemingly different worlds (particles and waves), it is one long, ongoing saga. It started with Kepler’s optics, continued with the rival optical theories of Newton (particles) and Huygens, Euler, Young and Fresnel (wave theory), and reached a first peak with Hamilton. It burst into life again in 1905 with Einstein’s notion of the light quantum, then went through another remarkable transformation in Schrödinger’s 1926 discovery of wave mechanics. I believe this saga has not yet run its course, as I will explain in the next chapter.

Now we come to Hamilton’s next discovery – the explanation of Fermat’s principle of least time, the idea that did more than anything else to foster the development of the principle of least action.

Figure 46 shows the wave crests of a light wave in a medium in which the speed of light is the same in all directions but varies from point to point, causing the wave crests to bend. The speed of light is less where the crests are closer together. Obviously, if some particle wanted to get from A to F in the least time, travelling always at the local speed of light, it would follow the curve ABCDEF . The individual segments of this curve are always perpendicular to the wave crests, and any deviation would result in a longer travel time. But this is also exactly the route a light ray would follow, cutting the wave crests at right angles. This was another great discovery that Hamilton made – that when geometrical optics holds, the wave theory of light can explain both Fermat’s principle of least time and Kepler’s light rays. The rays follow the lines of least travel time, and these are simultaneously the lines that always run perpendicular to the wave crests.

One of the most interesting things about geometrical optics is a connection it establishes with particles in Newtonian mechanics. The characteristic property of a moving particle is that it traces out a path through space. When regular wave patterns are present, wave theory creates similar one-dimensional tracks without any particles being present at all – the tracks of the light rays. Of course, in a strict wave theory the rays are not really ‘there’, but they are present as theoretical constructs. And many phenomena can be explained rather well by assuming that particles really are there. As John Wheeler would say, one has ‘particles without particles’, or even ‘histories without histories’.

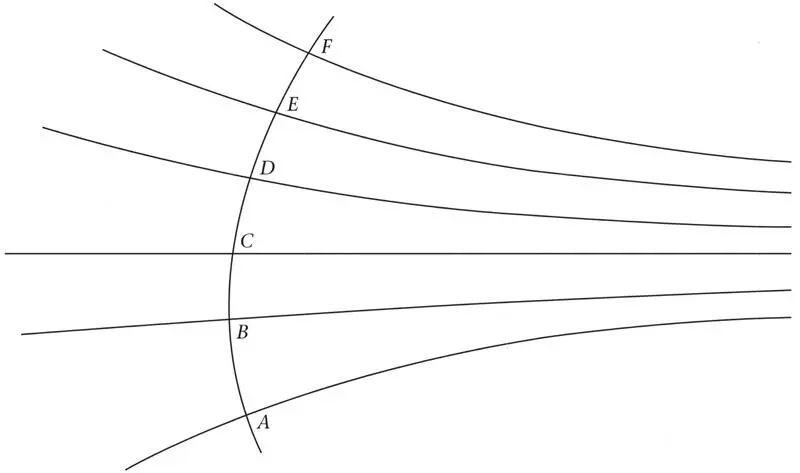
Figure 46.The explanation of Fermat’s principle of least time under the conditions of a regular wave pattern, so that geometrical optics holds.

In fact, work that Hamilton did about ten years after his optical discoveries shows how apt such a ‘Wheelerism’ is. As we saw in Part 2, classical physics is the story of paths in configuration spaces. They are Newtonian histories. Hamilton thought about what would happen if for them only one value of the energy is allowed, and made a remarkable discovery. He found that just as light rays, which are paths, arise from the wave theory of light when there is a regular wave pattern, the paths of Newtonian dynamical systems can arise in a similar fashion. I need to spell this out.