Julian Barbour - The End of Time - The Next Revolution in Physics

BOX 14 The Semiclassical Approach

This box provides some necessary details about the semiclassical approach. It is important here that the quantum wave function is not one wave pattern but two (the red and green ‘mists’). I mentioned the ‘tennis’ played between them – the rate of change in time of the red mist is determined by the curvatures of the green mist, and vice versa. This leads to the characteristic form of a momentum eigenstate, in which both mists have perfectly regular wave behaviour but with wave crests displaced relative to each other by a quarter of a wavelength. If the red crests are a quarter of a wavelength ahead of the green crests, the waves propagate in one direction and the momentum is in that direction. If the red crests are a quarter of a wavelength behind, the waves travel in the opposite direction and the momentum is reversed. We can call this phase locking . In a momentum eigenstate, there is perfect phase locking.

The semiclassical approach shows how two approximately phase-locked static waves can mimic evolution described by the time-dependent Schrödinger equation. In Figure 44 each of the two-dimensional wave patterns is nearly sinusoidal, and they are approximately phase-locked. These waves, being solutions of the stationary Schrödinger equation, are static – they do not move. But there is nothing to stop us (as in the example of the waves on the beach) from calling the direction along the axis perpendicular to the wave crests ‘time’ and the direction along the crests ‘space’.

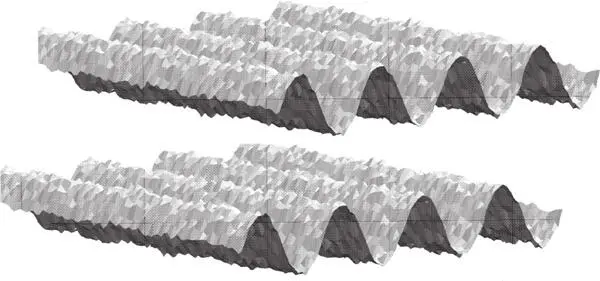
Figure 44.Two nearly sinusoidal wave patterns.

The key step now is to divide the total pattern of each wave into a regular part, corresponding to an imagined perfectly sinusoidal behaviour, and a remainder that is the difference between it and the actual (nearly sinusoidal) behaviour. Call this the difference pattern (there is one for each mist). If the condition of approximate phase locking holds, it turns out that the difference patterns satisfy with respect to our ‘space’ and ‘time’ an equation of the same form as the time-dependent Schrödinger equation, except for the appearance of one additional term. This term will have less and less importance, though, the more closely the assumptions of the semiclassical approach are satisfied.

In fact, the semiclassical approach offers the prospect of an explanation of time – in all its manifestations. It begins with a unified concept of things. Each point of Platonia is one distinct logically possible structure – it is one thing. The rules that make the structures make everything. Platonia is entire and eternal. No place in it is different from any other place, considered as something that is logically possible. But each structure is still a distinct individual. We see before us a true landscape whose every point is marked of necessity by individuality. It has striking topographic features. So there is a landscape, but nothing of a quite different nature that one might call time.

There is, though, one quite different element: a wave function. Schrödinger’s enigmatic ψ covers Platonia. Mist hovers over the eternal landscape. The static mist is a well-behaved solution – an eigenfunction – of the Wheeler-DeWitt equation. There is nothing here an unsuspecting bystander could say looks like time. You have seen mist on a landscape. Did it enter your head that such a thing could explain time? But it can, in principle. The static wave function, simply by its well-behaved response to the landscape it finds, may be induced into a regular wave-like pattern. If so, time can ‘emerge’ from timelessness. We shall see how the wave function enables the logically possible structures to interact – in a very real sense – with each other, thereby helping each other into an actual existence that seems to be deeply marked by time.

This ‘marking with time’ brings us to the tricky part in the semiclassical approach. It is what led me to the notion of time capsules. This is a point at which my ideas part company from (comparative) orthodoxy. Two closely related difficulties convinced me that a radical step was needed. The first arises from a significant difference between the two Schrödinger equations. The complex time-dependent equation is actually two equations for two separate components – the red and the green mist. They play a kind of ‘tennis’ which tightly couples their behaviour and creates phase locking in any semiclassical solution. In contrast, the stationary equation is usually a real equation which does not couple the two components of the wave function.

The existence of two separate yet almost perfectly matched wave patterns is crucial in the semiclassical approach. The waves must be parallel, and the wave crests displaced by a quarter of a wavelength. In standard quantum mechanics this is a valid assumption. Indeed, it is imposed because the true primary equation is the time-dependent Schrödinger equation. The secondary stationary equation is just a short cut to tell us the distribution of the blue mist without having to find the red and green mists first. But they are there, and they are of necessity phase-locked.

But quantum cosmology gives us only the Wheeler-DeWitt equation. It is the primary equation, but as it stands it will give only a blue mist. We cannot assume some deeper equation hiding behind it that will give phase-locked red and green mists. The truth is that this part of the semiclassical approach assumes something that should be derived. Luckily, this difficulty threatens to undermine only that part of the semiclassical approach in which the specific structure of the time-dependent Schrödinger equation is recovered. The broad picture in which ‘time’ emerges from timelessness is not threatened. In fact, complex numbers, which appear in my account in the guise of the red and green mists, are so deeply ingrained in quantum mechanics that I feel fairly confident that this problem will be sorted out. What is needed is some independent argument which enforces the appearance of a complex wave function and a coupling between its components. That would then ensure the necessary phase locking.

Nevertheless, we must take care not to introduce inadvertently into quantum cosmology assumptions that may be valid only in ordinary quantum mechanics. This brings me to the second difficulty with the semiclassical approach. It concerns motion and our conviction that we experience it, and simultaneously the issue of where our sense of the passage of time comes from. To understand the answer to this question is to understand time. It is all very well for me to speak about static wave patterns in a mist that hangs over Platonia. Such patterns will indeed, where they are sufficiently regular, define unambiguously a direction that may be called ‘time’. But even if the wave pattern is rather regular, we could not look at it and say that it distinguishes a direction of time. The one direction at right angles to the wave crests will look the same whichever way we face. There will be no signs set up on the distant horizons saying PAST and FUTURE. This is the issue we must now address.

It will be helpful to think about what it is that determines which way quantum wave packets move. Quantum mechanics is very different from classical mechanics in this respect. A classical initial condition consists of an initial position and an initial velocity. You know which way a particle will move because it is specified in the velocity. However, in quantum mechanics the initial condition is simply the values of the two components of the wave function, the red and green mists, everywhere at the initial time. Data like this seem to correspond to giving only the position in classical mechanics. Yet wave packets move under the rules Schrödinger prescribed.