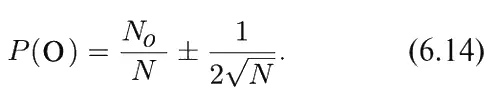
При такой записи подразумевается, что существует некая «истинная» вероятность, которую в принципе можно подсчитать , но что различные флуктуации приводят к ошибке при экспериментальном ее определении. Однако нет возможности сделать эти рассуждения логически согласованными. Лучше все-таки, чтобы вы поняли, что вероятность в каком-то смысле – вещь субъективная, что она всегда основывается на какой-то неопределенности наших познаний и величина ее колеблется при их изменении.
§ 4. Распределение вероятностей
Давайте вернемся к проблеме случайных блужданий, но теперь уже с некоторым изменением. Пусть в дополнение к случайному выбору направления шага (+ или −) некоторым непредсказуемым образом меняется также и его длина , причем требуется выполнение одного-единственного условия, чтобы длина шага в среднем была равна единице. Эта задача уже больше похожа на тепловое движение молекул в газе. Обозначим длину шага через S , которая, вообще говоря, может быть любой, но наиболее часто будет принимать значения где-то «вблизи» единицы. Для большей определенности давайте положим < S 2> = 1, или, что эквивалентно, S CK = 1. Вывод выражения для < D 2> при этом останется тем же, за исключением того, что уравнение (6.8) изменится теперь следующим образом:
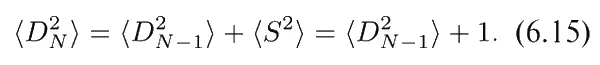
Так что, как и прежде,

Каково же в этом случае будет распределение расстояний! Какова, например, вероятность того, что после 30 шагов D окажется равным нулю? Вероятность этого равна нулю! Вообще вероятность любой заданной величины D равна нулю. Действительно, совершенно невероятно, чтобы сумма всех шагов назад (при произвольной длине каждого из них) в точности скомпенсировалась шагами вперед. В этом случае мы уже не можем построить график типа изображенного на фиг. 6.2.
Если же, однако, не требовать, чтобы D было в точности равно, скажем, нулю, или единице, или двум, а вместо этого говорить о вероятности получения D где-то вблизи нуля, или единицы, или двух, то при этом мы можем нарисовать график, подобный приведенному на фиг. 6.2. Назовем Р ( х, Δ x ) вероятностью того, что D будет находиться где-то внутри интервала Δ x в окрестности величины х (скажем, где-то между х и х + Δ x ). Если Δ x достаточно мало, то вероятность того, что D попадет в этот интервал, должна быть пропорциональна его ширине, т. е. Δ x . Поэтому мы можем утверждать, что
Р ( х , Δ х ) = р ( х ) Δ x. (6.17)
Функция р ( х ) называется плотностью вероятности.
Вид кривой р ( х ) зависит как от числа шагов N , так и от распределения шагов по длинам (т. е. от того, какую долю составляют шаги данной длины). К сожалению, я не могу здесь заниматься доказательством этого, а только скажу, что при достаточно большом числе шагов N плотность р ( х ) одинакова для всех разумных распределений шагов по длинам и зависит лишь от самого N. На фиг. 6.7 показаны три графика р ( х ) для различных N.
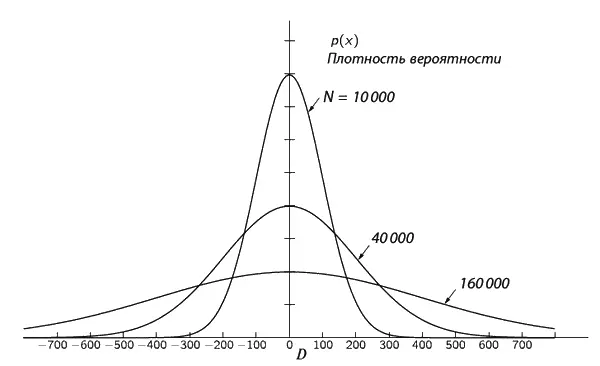
Фиг. 6.7. Плотность вероятности оказаться при случайном блуждании через N шагов на расстоянии D.
D измеряется в единицах средней квадратичной длины шага.
Заметьте, что «полуширины» этих кривых, как это и должно быть по нашим предыдущим расчетам, приблизительно равны √ N .
Вы, вероятно, заметили также, что величина р ( х ) вблизи нуля обратно пропорциональна √ N . Это происходит потому, что все кривые по форме очень похожи, только одни «размазаны» больше, а другие – меньше, и, кроме того, площади, ограниченные каждой кривой и осью х , должны быть равны. Действительно, ведь р ( х )Δ x ; это вероятность того, что D находится где-то внутри интервала Δ x (Δ x мало). Как определить вероятность того, что D находится где-то между x 1и x 2? Для этого разобьем интервал между x 1и x 2на узкие полоски шириной Δ x (фиг. 6.8) и вычислим сумму членов р ( х )Δ x для каждой такой полоски.
Читать дальше
![Ричард Фейнман Фейнмановские лекции по физике. Современная наука о природе [litres] обложка книги](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-cover.webp)
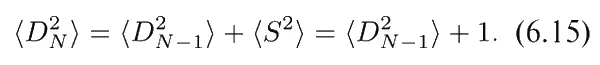







![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
