Можно спросить: а какова вероятность того, что в серии из 30 испытаний «орел» выпадет 15 раз или 16, или какое-то другое число раз? Мы говорим, что вероятность выпадения «орла» в серии из одного испытания равна 0,5; соответственно вероятность невыпадения тоже равна 0,5. В серии из двух испытаний возможны четыре исхода: ОО, OP, PO, PP. Так как каждый из них равновероятен, то можно заключить: а) вероятность двух выпадений «орла» равна 1/ 4; б) вероятность одного выпадения «орла» равна 2/ 4; в) вероятность невыпадения «орла» равна 1/ 2. Это происходит потому, что существуют две возможности из четырех равных получить одно выпадение «орла» и только одна возможность получить два выпадения или не получить ни одного.
Рассмотрим теперь серию из трех испытаний. Третье испытание с равной вероятностью может дать либо «орел», либо «решку», поэтому существует только один способ получения трех выпадений «орла»: мы должны получить два выпадения «орла» в двух первых испытаниях и затем выпадение «орла» в последнем. Однако получить два выпадения «орла» можно уже тремя способами: после двух выпадений «орла» может выпасть «решка» и еще два способа – после одного выпадения «орла» в первых двух испытаниях выпадет «орел» в третьем. Так что число равновероятных способов получить 3, 2, 1 и 0 выпадений «орла» будет соответственно равно 1, 3, 3 и 1; полное же число всех возможных способов равно 8. Таким образом, получаются следующие вероятности: 1/ 8, 3/ 8, 3/ 8, 1/ 8.
Эти результаты удобно записать в виде диаграммы (фиг. 6.3).
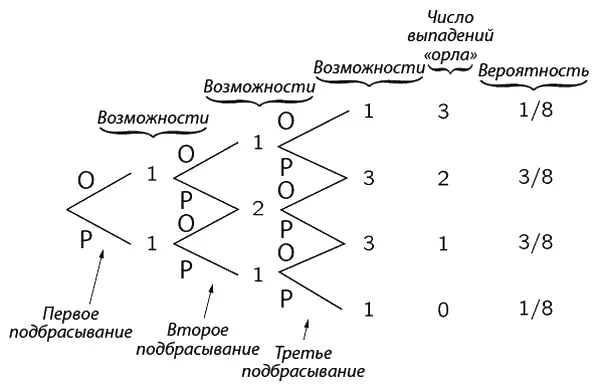
Фиг. 6.3. Диаграмма, иллюстрирующая число различных возможностей получения 0, 1, 2 и 3 выпадений «орла» в серии из трех испытаний.
Ясно, что эту диаграмму можно продолжить, если мы интересуемся еще бóльшим числом испытаний. На фиг. 6.4 приведена аналогичная диаграмма для шести испытаний.
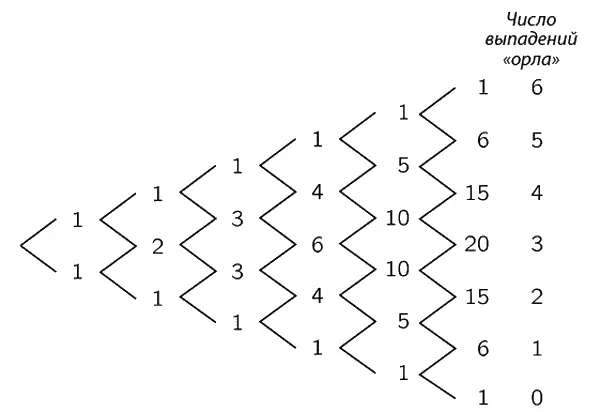
Фиг. 6.4. Диаграмма, подобная изображенной на фиг. 6.3, для серии из шести испытаний.
Число «способов», соответствующих каждой точке диаграммы, – это просто число различных «путей» (т. е., попросту говоря, последовательность выпадения «орла» и «решки»), которыми можно прийти в эту точку из начальной, не возвращаясь при этом назад, а высота этой точки дает общее число выпадений «орла». Этот набор чисел известен под названием треугольника Паскаля , а сами числа называются биномиальными коэффициентами , поскольку они появляются при разложении выражения ( a + b ) n . Обычно эти числа на нашей диаграмме обозначаются символом 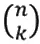 , или
, или 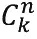 (число сочетаний из n по k ), где n – полное число испытаний, а k – число выпадений «орла». Отмечу попутно, что биномиальные коэффициенты можно вычислять по формуле
(число сочетаний из n по k ), где n – полное число испытаний, а k – число выпадений «орла». Отмечу попутно, что биномиальные коэффициенты можно вычислять по формуле

где символ n ! называемый « n -факториалом», обозначает произведение всех целых чисел от 1 до n , т. е. 1 ∙2 ∙3… ( n – 1) ∙ n.
Теперь уже все готово для того, чтобы с помощью выражения (6.1) подсчитать вероятность P ( k, n ) выпадения k раз «орла» в серии из n испытаний. Полное число всех возможностей будет 2 n (поскольку в каждом испытании возможны два исхода), а число равновероятных комбинаций, в которых выпадет «орел», будет 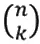 , так что
, так что
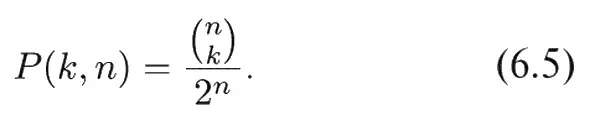
Поскольку P ( k, n ) – доля тех серий испытаний, в которых выпадение «орла» ожидается k раз, то из ста серий k выпадений «орла» ожидается 100 P ( k, n ) раз. Пунктирная кривая на фиг. 6.2 проведена как раз через точки функции 100 P ( k , 30). Видите, мы ожидали получить 15 выпадений «орла» в 14 или 15 сериях испытаний, а получили только в 13. Мы ожидали получить 16 выпадений «орла» в 13 или 14 сериях испытаний, а получили в 16. Но такие флуктуации вполне допускаются «правилами игры».
Использованный здесь метод можно применять и в более общей ситуации, где в каждом единичном испытании возможны только два исхода, которые давайте обозначим через В (выигрыш) и П (проигрыш). Вообще говоря, вероятности В и П в каждом отдельном испытании могут быть разными. Пусть р , например, будет вероятностью результата В. Тогда q (вероятность результата П) должна быть равна (1 – p ). В серии из n испытаний вероятность того, что результат В получится k раз, равна
Читать дальше
![Ричард Фейнман Фейнмановские лекции по физике. Современная наука о природе [litres] обложка книги](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-cover.webp)


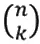 , или
, или 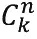 (число сочетаний из n по k ), где n – полное число испытаний, а k – число выпадений «орла». Отмечу попутно, что биномиальные коэффициенты можно вычислять по формуле
(число сочетаний из n по k ), где n – полное число испытаний, а k – число выпадений «орла». Отмечу попутно, что биномиальные коэффициенты можно вычислять по формуле
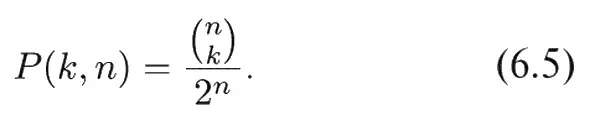





![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
