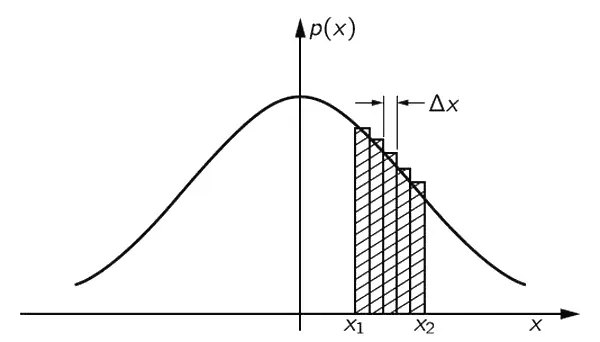
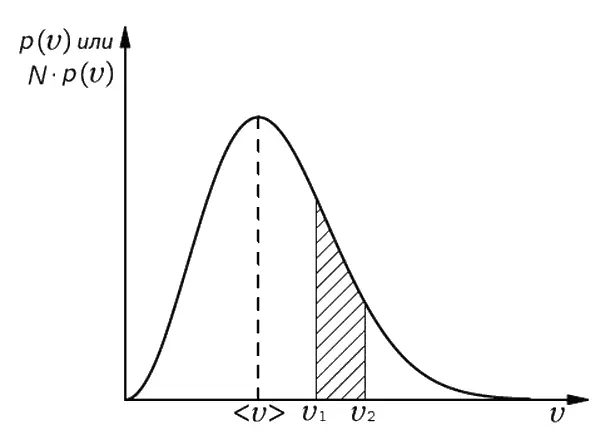
Фиг. 6.8. Вероятность [заштрихованная область под кривой р(х)] того, что при случайном блуждании пройденное расстояние D окажется между x 1и x 2.
Геометрически эта вероятность [запишем ее в виде P ( x 1< D < x 2)] равна площади заштрихованной области на фиг. 6.8. При этом чем ýже будут наши полоски, тем точнее результат. Поэтому можно записать
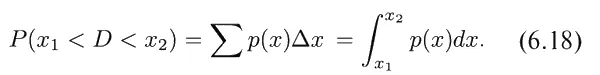
Площадь же ограничения всей кривой просто равна вероятности того, что D принимает какое-то значение между −∞ и +∞. Ясно, что она должна быть равна единице, т. е.
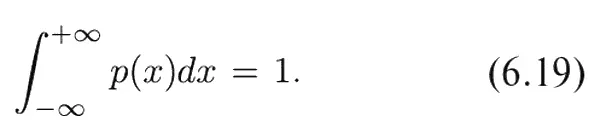
Ну а поскольку ширина кривых на фиг. 6.7 пропорциональна √ N , то, чтобы сохранить ту же площадь, их высота должна быть пропорциональна 1/√ N .
Плотность вероятности, которую мы только что описали, встречается наиболее часто. Она известна также под названием нормальной , или гауссовой , плотности вероятности и записывается в виде
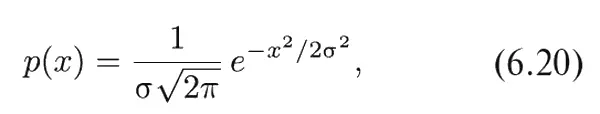
причем величина σ называется стандартным отклонением.
В нашем случае σ = √ N или √ N S CK, если средняя квадратичная длина шага отлична от единицы.
Мы уже говорили о том, что движения молекул или каких-то других частиц в газе похожи на случайные блуждания. Представьте себе, что мы открыли в комнате пузырек с духами или каким-то другим органическим веществом. Тотчас же молекулы его начнут испаряться в воздух. Если в комнате есть какие-то воздушные течения, скажем циркуляция воздуха, то они будут переносить с собой пары этого вещества. Но даже в совершенно спокойном воздухе молекулы будут распространяться, пока не проникнут во все уголки комнаты. Это можно определить по запаху или цвету. Если нам известен средний размер «шага» и число шагов в секунду, то можно подсчитать вероятность обнаружения одной или нескольких молекул вещества на некотором расстоянии от пузырька через какой-то промежуток времени. С течением времени число шагов возрастает и газ «расползается» по комнате, подобно нашим кривым на фиг. 6.7. Длина шагов и их частота, как вы узнаете впоследствии, связаны с температурой и давлением воздуха в комнате.
Вы знаете, что давление газа вызывается тем, что молекулы его бомбардируют стенки сосуда. Позднее, когда мы подойдем к количественному описанию этого явления, нам понадобится знать, с какой скоростью движутся молекулы, ударяясь о стенку, поскольку сила их ударов зависит от скорости. Однако говорить о какой-то определенной скорости молекул совершенно невозможно. В этом случае необходимо использовать вероятностное описание. Молекула может иметь любую скорость, но некоторые скорости предпочтительнее других. Все происходящее в газе можно описать, сказав, что вероятность того, что данная молекула движется с какой-то скоростью между υ и υ + Δ υ , будет равна p ( υ ) Δ υ , где p ( υ ) – плотность вероятности, которая зависит от скорости υ . Позднее я расскажу, как Максвелл, используя общие понятия и идеи теории вероятности, нашел математическое выражение для функции p ( υ ) [7] Максвелл получил выражение p ( υ ) = Cυ 2 e − aυ2 , где а – некоторая связанная с температурой постоянная, а С выбирается таким образом, чтобы полная вероятность была равна единице.
. Примерный вид функции p ( υ )показан на фиг. 6.9.
Фиг. 6.9. Распределение молекул газа по скоростям.
Скорость может иметь любую величину, однако больше шансов за то, что она окажется где-то в окрестности наиболее вероятного или ожидаемого значения < υ >.
О кривой, показанной на фиг. 6.9, часто говорят в несколько ином смысле. Если мы возьмем газ, заключенный в каком-то сосуде (скажем, объемом 1 л ), то окажется, что в нем имеется огромное количество молекул ( N ≈ 10 22). Поскольку p ( υ) Δ υ – вероятность того, что первая попавшаяся молекула будет лететь со скоростью, находящейся в интервале Δ υ , то, по определению, ожидаемое число молекул <���Δ N > со скоростью, находящейся в этом же интервале, будет равно
Читать дальше
![Ричард Фейнман Фейнмановские лекции по физике. Современная наука о природе [litres] обложка книги](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-cover.webp)

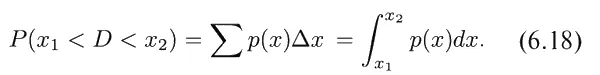
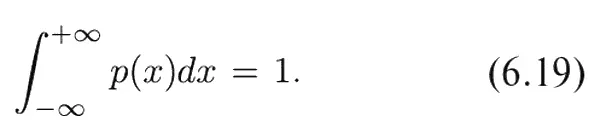
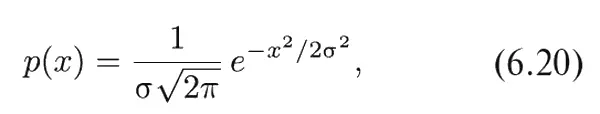






![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
