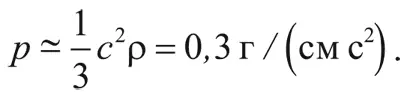
Следовательно, масса Джинса была:

Интересно отметить, что крупные шаровые скопления в нашей Галактике имеют примерно такую же массу.
Заметка 6. Температура и плотность нейтрино
Если тепловое равновесие не нарушается, в системе сохраняется физическая величина, известная как энтропия. Для наших целей достаточно будет воспользоваться приближенной формулой для энтропии S в единице объема при температуре T :
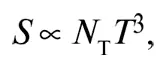
где Ν Τ – эффективное число сортов частиц, находящихся в тепловом равновесии, температурный порог которых ниже Τ . Чтобы сохранить энтропию на постоянном уровне, надо, чтобы S была обратно пропорциональна кубу размера Вселенной. Другими словами, если R – расстояние между любой парой типичных галактик, то:
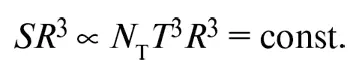
Незадолго до аннигиляции электронов и позитронов (при температуре около 5 × 10 9K) нейтрино и антинейтрино уже вышли из теплового контакта с веществом во Вселенной, поэтому единственными частицами в тепловой бане оставались электрон, позитрон и фотон. Возьмем из таблицы I на с. 212 полное эффективное число сортов частиц до аннигиляции:
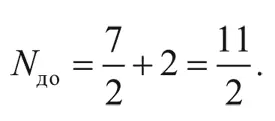
После того как в четвертом стоп-кадре электроны и позитроны аннигилировали, во Вселенной стали преобладать фотоны. Таким образом, число сортов стало:
N после= 2.
Из сохранения энтропии следует, что:
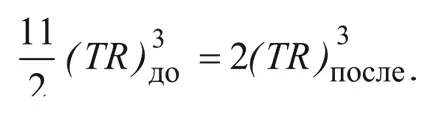
То есть тепло, выделившееся в процессе аннигиляции электронов и позитронов, приводит к повышению величины TR на коэффициент:
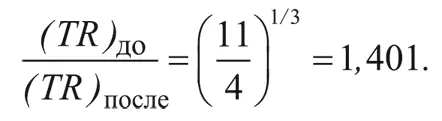
До аннигиляции электронов с позитронами температура нейтрино Τ была равна температуре фотонов Τ. Но затем Τ v начала падать просто как 1/ R , поэтому в любой последующий момент времени T v R равно значению TR до аннигиляции:
(T v R) после = (T v R) до = (T v R) до.
Отсюда заключаем: после завершения процесса аннигиляции температура фотонов превышает температуру нейтрино на коэффициент:
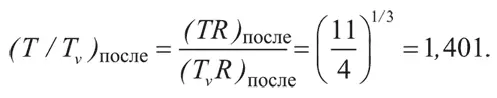
Хотя нейтрино и антинейтрино вышли из теплового равновесия, они вносят существенный вклад в полную плотность энергии. Эффективное число сортов нейтрино равно 7/2, т. е. 7/4 от числа степеней свободы фотона. (Фотон может находиться в двух состояниях с разным спином.) А температура нейтрино в четвертой степени, наоборот, в (4/11) 4/3 раза меньше температуры фотонов в четвертой степени. Соответственно отношение плотности энергии нейтрино и антинейтрино к плотности энергии фотонов равно:
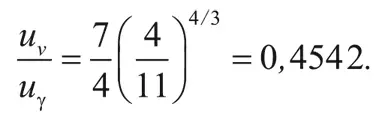
Из закона Стефана – Больцмана (см. главу 3) следует, что при температуре фотонов T плотность энергии фотонов есть:
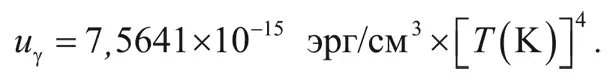
Таким образом, полная плотность энергии после аннигиляции электронов и позитронов равна:
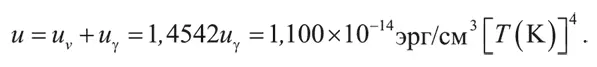
Эту величину можно пересчитать в массовую плотность, разделив первую на квадрат скорости света:
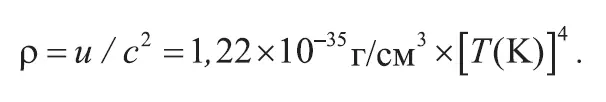
Послесловие. Что произошло в космологии с 1977 г.
За 16 лет, прошедших с момента первого издания «Первых трех минут», Вселенная расширилась на 12 стомиллионных процента. А может быть, только на 6,5 стомиллионных. Такой разброс данных связан с тем, что мы по-прежнему не очень точно знаем темп расширения Вселенной. Как говорилось в главе 2, он выражается через один из важнейших космологических параметров – постоянную Хаббла, которую измеряют, наблюдая зависимость скоростей далеких галактик от расстояния до них. В последнее время ошибки измерений, по словам астрономов, непрерывно уменьшаются. Однако разница между результатами различных групп, к сожалению, выходит за рамки заявленных погрешностей. По данным одних наблюдений, получена величина 80 км/с на мегапарсек (3,26 миллиона световых лет), а по другим, скорости галактик увеличиваются на 40 км/с на каждый мегапарсек. Получается, мы знаем темп расширения Вселенной всего лишь с точностью до двойки.
Читать дальше
![Стивен Вайнберг Первые три минуты [litres] обложка книги](/books/398000/stiven-vajnberg-pervye-tri-minuty-litres-cover.webp)

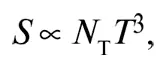
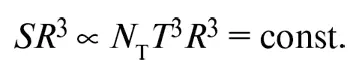
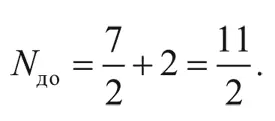
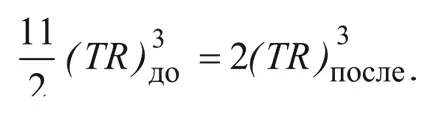
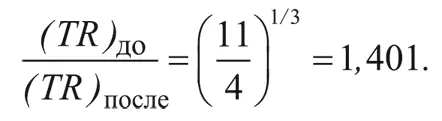
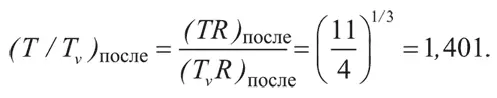
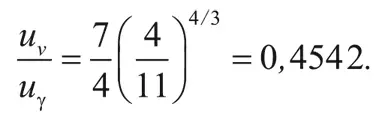
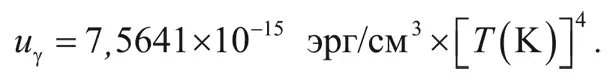
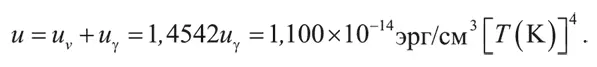
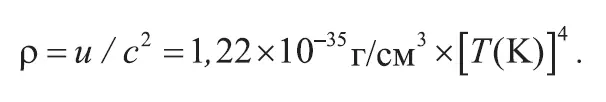







![Владимир Поселягин - Зург - Я – выживу. Становление. Империя [первая трилогия] [сборник litres]](/books/408870/vladimir-poselyagin-zurg-ya-vyzhivu-stanovlenie-thumb.webp)



