Если E отрицательна, то галактика никогда не уйдет на бесконечность, поскольку на больших расстояниях потенциальной энергией можно пренебречь. Тогда полная энергия оказывается практически равной кинетической, а та, в свою очередь, всегда положительна. С другой стороны, если E положительна, то галактика может достичь бесконечности с некоторым запасом кинетической энергии. Таким образом, энергия E галактики, движущейся со скоростью убегания, по определению равна нулю. Откуда следует, что:
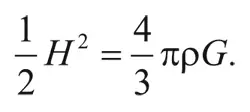
Другими словами, плотность должна равняться:
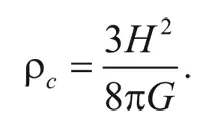
Это и есть критическая плотность. (Хотя мы получили этот результат в рамках ньютоновской физики, он применим и тогда, когда вещество во Вселенной обладает релятивистскими скоростями. Под ρ в таком случае понимается полная плотность энергии, деленная на с 2.)
Например, если взять общепринятое сегодня значение постоянной Хаббла (15 км/с на миллион световых лет), то, учитывая, что в световом годе 9,46 × 10 12километров, получим:
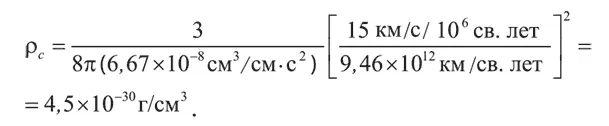
В одном грамме содержится 6,02 × 10 23нуклонов. Соответственно это значение критической плотности соответствует 2,7 × 10 –6нуклонам на кубический сантиметр, или 0,0027 частицы на литр.
Заметка 3. Оценки времени расширения
Рассмотрим теперь, как параметры Вселенной меняются со временем. Допустим, в момент времени t типичная галактика массой m находится на расстоянии R(t) от произвольно выбранного центра – например, от нашей Галактики. В предыдущей заметке мы показали, что полная (кинетическая и потенциальная) энергия такой галактики равна:
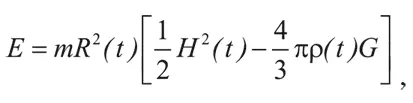
где H(t) и ρ( t ) – значения постоянной Хаббла и плотности вещества во Вселенной в момент времени t. Эта величина является постоянной. Однако мы скоро увидим, что ρ(t) при R(t) → 0 растет не медленнее, чем 1/ R 3 (t), поэтому ρ(t) R 2 (t) растет не медленнее, чем 1/ R(t), когда R(t) стремится к нулю. Чтобы результирующая энергия оставалась постоянной, два слагаемых в скобках должны быть почти равны. В итоге при R(t) → 0 имеем:

Характерное время расширения Вселенной есть величина, обратная постоянной Хаббла, т. е.:
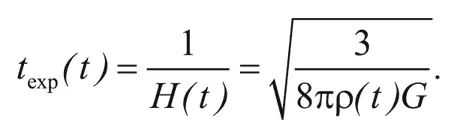
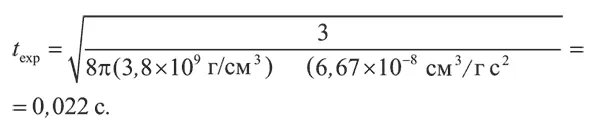
Например, в момент первого стоп-кадра в главе 5 плотность составляла 3,8 миллиарда грамм на кубический сантиметр. Таким образом, время расширения равнялось:
Зададимся вопросом: как ρ(t) зависит от R(t) ? Если основной вклад в плотность вносят нуклоны (материально-доминированная стадия), то полная масса внутри сопутствующей сферы радиуса R(t) пропорциональна количеству нуклонов внутри этой сферы и, следовательно, не меняется:
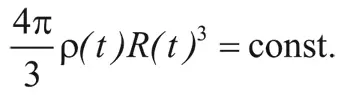
Следовательно, ρ(t) обратно пропорциональна R(t) 3 :
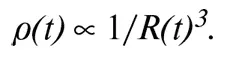
(Символ ∝ означает «пропорциональна».) Если же в плотности преобладает плотность (массовая) излучения (полученная из плотности энергии делением на скорость света в квадрате), что соответствует радиационно-доминированной эпохе, то p(t) пропорциональна четвертной степени температуры. Но температура меняется как 1/ R(t), а значит, ρ(t) обратно пропорциональна R(t) 4 :
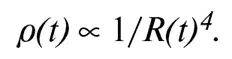
Чтобы одновременно учесть как материально-, так и радиационно-доминированную стадию, запишем этот результат в следующей форме:

Попутно заметим, что ρ(t) , как и следовало ожидать, действительно расходится не медленнее, чем 1/R(t) 3 при R( t ) → 0.
Читать дальше
![Стивен Вайнберг Первые три минуты [litres] обложка книги](/books/398000/stiven-vajnberg-pervye-tri-minuty-litres-cover.webp)
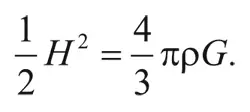
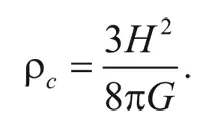
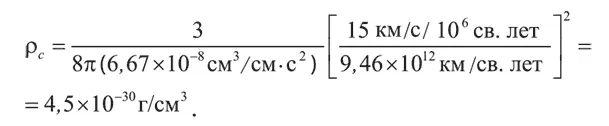
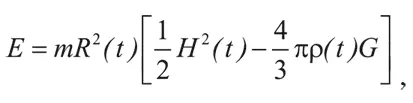

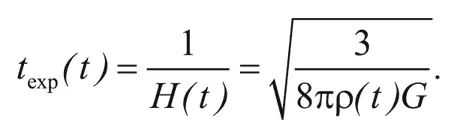

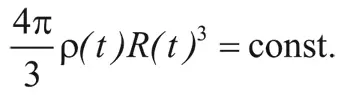
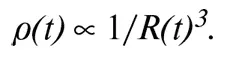
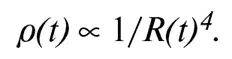








![Владимир Поселягин - Зург - Я – выживу. Становление. Империя [первая трилогия] [сборник litres]](/books/408870/vladimir-poselyagin-zurg-ya-vyzhivu-stanovlenie-thumb.webp)



