
Но скорость типичной галактики тогда равна:
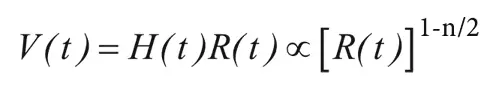
Из дифференциального исчисления хорошо известно, что если скорость пропорциональна какой-либо степени расстояния, то время, необходимое для перемещения из одной точки в другую, пропорционально изменению отношения расстояния к скорости. Говоря более точно, если V пропорциональна R(t) 1–n/2 , то промежуток времени

Таким образом, каково бы ни было значение n , истекшее время пропорционально разности обратных корней из плотности.
Например, после аннигиляции электронов и позитронов в течение всей радиационно-доминированной эпохи плотность энергии имеет следующий вид (см. математическую заметку 6 на с. 249):
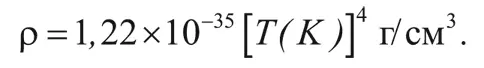
Кроме того, в последнем выражении п = 4. Таким образом, Вселенная охлаждается от 100 до 10 миллионов градусов за:
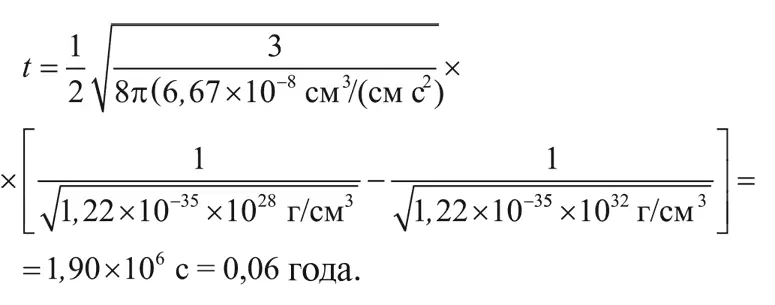
Полученный общий результат более прозрачно можно сформулировать так: промежуток времени, за который плотность падает до ρ (с величины, много большей, чем ρ), равен:

(Если ρ ( t 2 ) > ρ ( t 1 ), то вторым членом в формуле для t 1 – t 2 можно пренебречь.) Например, при температуре 3000 K массовая плотность фотонов и нейтрино равнялась:
ρ = 1,22 × 10 –35× [3000] 4г/см 3= 9,9 × 10¯ 22г/см 3.
Это настолько мало по сравнению с плотностью при 10 8K (или 10 7K, или 10 6K), что время, за которое Вселенная охладится от очень высоких температур, царивших в первые мгновения ее жизни, до 3000 K, можно рассчитать (положив n = 4) следующим образом:

Мы показали, что промежуток времени, за которой плотность падает от экстремальных значений, имевших место в ранней Вселенной, до ρ пропорционален, а сама плотность ρ пропорциональна 1/ R n. Время, следовательно, пропорционально R n/2, или, что то же самое:

Эта формула остается в силе до тех пор, пока кинетическая и потенциальная энергии не упадут настолько, что достигнут одного порядка с их суммой – полной энергией.
Как было отмечено в главе 2, в любой момент времени t на расстоянии ct существует горизонт, отсекающий сигналы, которые еще не успели до нас дойти. Теперь мы увидели, что R(t) при t → 0 уменьшается медленнее, чем расстояние до горизонта. То есть в прошлом был момент, когда все «типичные» частицы находились за горизонтом.
Заметка 4. Излучение абсолютно черного тела
Согласно планковскому распределению энергия du чернотельного излучения в единице объема и в узком интервале длин волн от λ до λ + dλ равна:
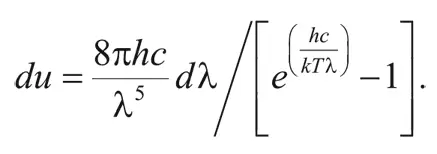
Здесь T – температура, k – постоянная Больцмана (1,38 × 10¯ 16эрг/K), c – скорость света (299 729 км/с), e – число, равное 2,718…, и h – постоянная Планка (6,625 × 10¯ 27эрг с), которую в эту формулу ввел Макс Планк.
В случае длинных волн для знаменателя в формуле Планка верно приближенное равенство:
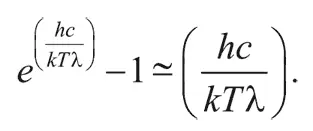
Таким образом, в данном диапазоне длин волн планковское распределение сводится к виду:
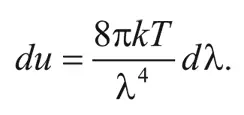
Эта формула выражает закон Рэлея – Джинса. Если бы он соблюдался для сколь угодно коротких волн, производная du/dλ стремилась бы к бесконечности при λ→0 и полная плотность энергии чернотельного излучения была бы бесконечной.
К счастью, планковское распределение достигает максимума при длине волны:
Читать дальше
![Стивен Вайнберг Первые три минуты [litres] обложка книги](/books/398000/stiven-vajnberg-pervye-tri-minuty-litres-cover.webp)

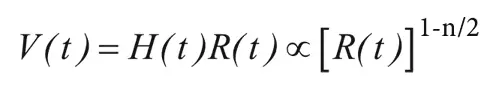

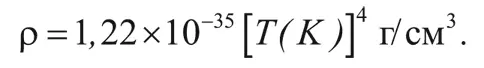
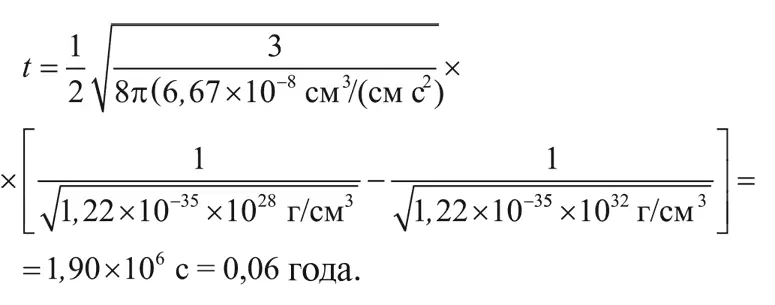



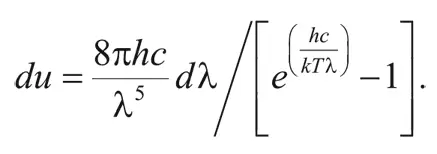
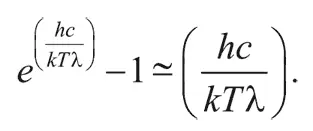
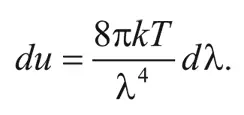







![Владимир Поселягин - Зург - Я – выживу. Становление. Империя [первая трилогия] [сборник litres]](/books/408870/vladimir-poselyagin-zurg-ya-vyzhivu-stanovlenie-thumb.webp)



