Колебания пружины и пузырька
В положении равновесия форма воздушного пузырька небольшого размера в воде является сферической. Его радиус таков, что давление воздуха внутри пузырька компенсирует давление воды. В результате внешнего воздействия (например, звуковой волны) пузырь деформируется и затем начинает колебаться около своего равновесного положения.
Эти колебания могут быть представлены в виде суммы большого числа различных деформационных мод. Некоторые из них приводят к значительным смещениям поверхности пузыря; такие моды называют резонансными. Один из таких резонансов, резонанс Миннарта, происходит на весьма низкой частоте: при этом он соответствует возбуждению звуковых волн весьма больших длин (как в воздухе, так и в воде) по сравнению с размерами самого колеблющегося пузырька. Эти колебания оказываются аналогичными колебаниям подвешенного на пружине и выведенного из положения равновесия шара (см. илл. ниже): при отсутствии затухания шар начинает колебаться с определенной частотой ƒ, которая зависит только от величины его массы и жесткости k пружины. Чтобы понять аналогию с пузырьком, заметим, что масса шара M в случае пузырька соответствует массе вовлеченной в движение жидкости, в то время как роль возвращающей силы упругости пружины в случае пузырька играет сила избыточного давления, стремящаяся вернуть его поверхность в положение равновесия. В случае пружины эта сила пропорциональна удлинению x пружины: F = – kx , где постоянная k является характеристикой пружины. Частота колебаний шара равна
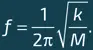
Она тем выше, чем жестче пружина и меньше масса.
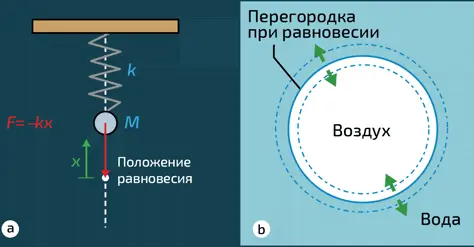
Колебания подвешенного на пружине шара (a) аналогичны колебаниям пузырька (b), который осциллирует между двумя крайними позициями (пунктирные окружности) около своего равновесного положения (сплошная линия)
А какой же будет формула для колебаний пузырька? Воспользуемся методом размерности и подберем для пузырька характерные физические параметры, которые заменят M и k . Таким образом мы немного сократим сложный расчет (который, однако, остается необходимым для получения точного количественного результата). Характерные величины, которые, очевидно, должны войти в ответ, – это плотность ρ жидкости, радиус пузырька R в положении равновесия и начальное давление жидкости P . Действительно, возвращающая сила, воздействующая на поверхность пузыря, возникает из-за давления внутри него, которое в равновесном положении должно быть равным давлению жидкости. Масса же вовлеченной в движение жидкости по порядку величины соответствует произведению объема пузырька на ее плотность: (4/3)π R 3ρ. Что же касается коэффициента жесткости k , то он должен представлять собой отношение возвращающей силы к длине. Единственная величина, имеющая размерность длины в нашей задаче, – это радиус R , а величина с размерностью силы – это произведение давления P на площадь поверхности пузыря, то есть PR 2. Таким образом, коэффициент жесткости k должен быть порядка PR . Подставив эти значения в предыдущую формулу, получим результат, близкий к выражению, которое вывел Марсел Миннарт:
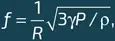
где для пузырька воздуха γ = 7/5. Поверхностное натяжение σ в эту формулу не вошло: его роль становится существенной лишь в случае достаточно малых пузырьков.
Эти наблюдения, сделанные в результате произнесения авторами многочисленных тостов, тем не менее остаются эмпирическими. Эксперименты, проведенные в Университете Париж VII, позволили более точно изучить распространение звука в газированной жидкости. Исследователи, очевидно, использовали для своих экспериментов не шампанское, а содержащую пузырьки воздуха воду. Они обнаружили, что достаточно даже низкой концентрации воздушных пузырьков (порядка одного пузырька диаметром в миллиметр на кубический сантиметр жидкости), чтобы снизить скорость звука в несколько раз (порядка 10) и существенно смягчить слышимый звук. Влияние наличия пузырьков на скорость звука легко выяснить: последняя определяется комбинацией 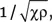 где χ – сжимаемость (адиабатическая) среды, а ρ – ее плотность. Наличие небольшого количества пузырьков мало влияет на плотность жидкости (в рассмотренном выше случае – шампанского), в то время как сжимаемость, крайне низкая при отсутствии пузырьков, с их добавлением заметно увеличивается. Что же касается затухания звука в слышимом диапазоне, то это явление во многом связано с резонансом отдельных пузырей в жидкости. Ниже мы рассмотрим это явление подробнее.
где χ – сжимаемость (адиабатическая) среды, а ρ – ее плотность. Наличие небольшого количества пузырьков мало влияет на плотность жидкости (в рассмотренном выше случае – шампанского), в то время как сжимаемость, крайне низкая при отсутствии пузырьков, с их добавлением заметно увеличивается. Что же касается затухания звука в слышимом диапазоне, то это явление во многом связано с резонансом отдельных пузырей в жидкости. Ниже мы рассмотрим это явление подробнее.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

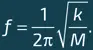

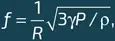
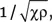 где χ – сжимаемость (адиабатическая) среды, а ρ – ее плотность. Наличие небольшого количества пузырьков мало влияет на плотность жидкости (в рассмотренном выше случае – шампанского), в то время как сжимаемость, крайне низкая при отсутствии пузырьков, с их добавлением заметно увеличивается. Что же касается затухания звука в слышимом диапазоне, то это явление во многом связано с резонансом отдельных пузырей в жидкости. Ниже мы рассмотрим это явление подробнее.
где χ – сжимаемость (адиабатическая) среды, а ρ – ее плотность. Наличие небольшого количества пузырьков мало влияет на плотность жидкости (в рассмотренном выше случае – шампанского), в то время как сжимаемость, крайне низкая при отсутствии пузырьков, с их добавлением заметно увеличивается. Что же касается затухания звука в слышимом диапазоне, то это явление во многом связано с резонансом отдельных пузырей в жидкости. Ниже мы рассмотрим это явление подробнее.


![Лина Сайфер - Театр мыльных пузырей [litres]](/books/434478/lina-sajfer-teatr-mylnyh-puzyrej-litres-thumb.webp)






