Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

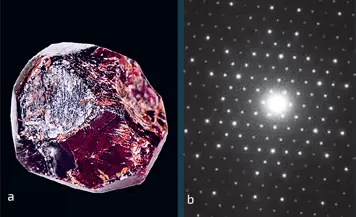
a. Гранат. b.Дифрактограмма граната. Расположение четких пятен дает нам информацию о расположении атомов внутри кристалла

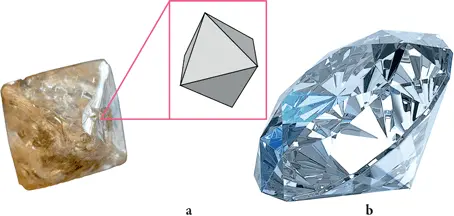
6. Этапы гранения необработанного октаэдрического алмаза (а). Чтобы получить бриллиант (b), огранщик начинает с небольшого надреза в камне, а затем ударяет по введенному в него лезвию, после чего алмаз раскалывается пополам по плоскости расщепления. Затем ювелир путем полировки создает грани (для получения бриллианта в современной огранке их должно быть 58)

С другой стороны, по определению кристалл остается неизменным при бесконечном количестве сдвигов: достаточно выбрать их расстояния и направления, которые соответствовали бы периодичности кристалла. Именно это свойство, трансляционная симметрия, сегодня считается наиболее характерным свойством кристаллов, а не их макроскопическая симметрия, наблюдаемая невооруженным глазом. Красота кристаллов, их сверкающие грани и причудливые формы не могут не восхищать нас, будь то маленький бриллиант в кольце или один из великолепных минералогических шедевров, которыми можно полюбоваться в музеях естественной истории.

Но, кстати, какова связь между микроскопической структурой кристалла и его макроскопической геометрией? Наличие плоских блестящих граней, будь они природными или полученными в результате обработки, – результат регулярности микроскопической структуры. На самом деле совсем не сложно расколоть кристалл, образовав гладкие плоскости: если одна атомная связь слаба, то все связи, имеющие аналогичное положение в кристаллической решетке, будут столь же слабыми. Эту особенность кристаллов используют ювелиры при огранке необработанных алмазов (илл. 6). Формирование плоских граней при росте кристалла может быть объяснено аналогичным образом.

Кристаллы могут иметь оси симметрии порядков 2, 3, 4 или 6… но только не пятого порядка! Исключение числа 5 из этого списка – математически неоспоримое свойство: невозможно заполнить пространство повторяющейся ячейкой с симметрией пятого порядка. Как было отмечено, на плоскости можно замостить тротуар прямоугольниками, шестиугольниками, квадратами или равносторонними треугольниками (см. главу 8, «Упаковка дисков и «замощение» плоскости многоугольниками»), но не пятиугольниками!

Эта аномалия интересует некоторых исследователей, тем более что сама природа, судя по всему, охотно принимает симметрию пятого порядка. Так, она часто встречается в цветах (илл. 7). Она возникает и в небольших скоплениях атомов, получаемых в лаборатории. Исследователям удается получить скопления молекул Al 13 или Al 12 C, образованных из одного центрального и 12 периферийных атомов: они формируют правильный икосаэдр, который имеет оси симметрии пятого порядка (см. илл. b в главе 8, врезке «Поцелуи» шаров в задаче Кеплера»), а не кубоктаэдр, являющийся элементарной ячейкой компактной укладки (илл. а в главе 8, врезке «Поцелуи» шаров в задаче Кеплера»).

Однако даже для бесконечной системы симметрия пятого порядка не является несовместимой с высокой компактностью. Если отказаться от построения периодической структуры с симметрией пятого порядка, то можно довольствоваться расположением, показанным на илл. 8, где шарики каждого слоя расположены на гранях правильных пятиугольников. Полученное заполнение составляет 72 %, что ненамного меньше возможной максимальной величины 74 % (см. главу 8, «Шары в реальном мире»).

7. Венчик колокольчика имеет симметрию пятого порядка

Теоретический запрет на существование кристаллов с симметрией пятого порядка был доказан давно, еще в работах кристаллографов XIX века. Поэтому, когда в 1984 году команда, возглавляемая Даном Шехтманом, задалась вопросом о структуре синтезированного в лаборатории сплава алюминия и марганца и провела дифрактометрию, ее результат был подобен грому среди ясного неба. Дифрактограмма этого материала, как и в случае с кристаллом, имела локализованные светлые пятна (илл. 9). Но – о ужас! – она показывала, что сплав имеет симметрию пятого порядка вопреки законам кристаллографии! Это вещество назвали «квазикристаллом» с «квазипериодической» структурой (см. главу 9, врезку «Оригинальная плитка для ванной…»). В 1991 году Международный союз кристаллографии (International Union of Crystallography, IUCr) определил его как «твердое тело без трехмерной периодичности», но с «по существу дискретной дифрактограммой», такой, как у кристаллов. Ярких пятен дифракционной картины действительно намного больше, чем в кристалле: на самом деле существует бесконечность для любой зоны дифракционной картины, большинство из которых настолько слабы, что почти невидимы.