Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Если же давление по обе стороны мыльной пленки оказывается разным, то она образует поверхности со средней кривизной, равной во всех точках, но отличной от нуля. Скажем, таковы мыльные пузыри, возникшие на проволочной раме и удерживающие воздух. Простым примером такой поверхности является замкнутый двумя сферическими «шапками» цилиндрический пузырь (илл. 9): его средняя кривизна γ везде равна 1/(2 R ), где R – радиус колец.

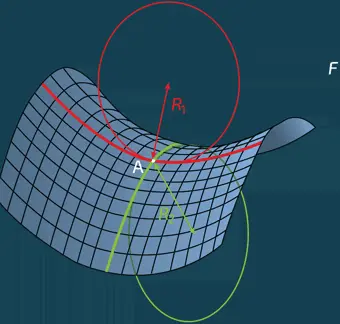
Геометрия минимальной поверхности (форма мыльной пленки, находящейся под равными давлениями со всех сторон). В любой точке A такой поверхности лежащие на ней кривые либо вогнуты (красная кривая), либо выпуклы (зеленая кривая). Красная кривая соответствует минимальной кривизне линии, уходящей вверх (вогнутой), а зеленая – минимальной кривизне линии, загибающейся вниз (выпуклой). Для минимальной поверхности обе кривизны 1/ R 1 и 1/ R 2 должны быть равны по модулю

Распаду струи предшествует появление выпуклостей и сужений, которые увеличиваются вплоть до отделения капель. Сверхбыстрая фотосъемка показывает, что между двумя каплями нормального размера образуется небольшая капля, подобная уже известному нам «шарику Плато». Действительно, прежде чем отделиться, большие капли разделяются длинным и тонким цилиндром, который после окончательного отделения капель и образует «шарик Плато». Поведение струи во времени оказывается довольно сложным. Капли становятся то удлиненными, то сплющенными, проходя промежуточную сферическую форму. Эти колебания можно изучать либо с помощью метода скоростной фотосъемки, либо куда более давним, изобретенным Плато методом стробоскопии, при котором движущийся объект освещается периодически, однако лишь в течение кратких мгновений.

Первые наблюдения за распадом струи жидкости под влиянием звука были выполнены французским физиком Феликсом Саваром (1791–1841), чьим именем впоследствии была названа единица измерения, используемая для оценки высоты музыкальных нот. Ученый заметил, что возбуждение вблизи струи музыкального звука подходящей частоты усиливает ее фрагментацию: цилиндрическая часть струи практически исчезает, она начинает делиться на капли с самого верха. Согласно Савару, будущие капли начинают формироваться в струе уже сразу после ее выхода из крана. Поначалу это простые выпуклости, становящиеся все более и более выраженными по мере падения жидкости до точки, где они полностью разделяются. Эти близкие друг к другу выпуклости (илл. 12) производят слабый, но четко определенной частоты звук. Ученый предположил, что музыкальная нота, звучащая в унисон с этими колебаниями, оказывает особое влияние на струю и разрывает ее на вереницу капель!

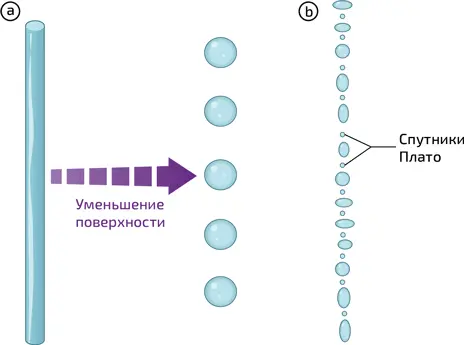
12. Тонкая цилиндрическая струя воды, чтобы минимизировать свою поверхностную энергию, распадается на капли (a). При определенных условиях между каждой парой больших капель возникает небольшая капелька (так называемый спутник Плато). Из-за деформации в момент отрыва капля падает колеблясь (b)

Британский физик Джон Тиндаль (1820–1893) продолжил опыты Савара с прозрачной цилиндрической струей 27-метровой высоты – такая струя под воздействием звука органной трубы становилась мутной и распадалась на множество капель. Тиндаль лил воду в широкий сосуд, располагая его на разной высоте, выше или ниже точки, в которой струя мутнела. Вот что он обнаружил: «Когда нисходящая струя пересекает поверхность жидкости выше “точки перерыва”, причем давление не слишком сильно, то она входит в нее молча; но когда эта поверхность пересекается со струей ниже точки перерыва, то слышится журчание и появляется множество пузырьков».

Приглашаем вас, дорогие читатели, провести два эксперимента на вашей кухне (необязательно доводя их до совершенства, как Плато; см. главу 6, «Капающий кран»).

Опыт 1

Устранение действия гравитации на капли

Наполните маслом узкий стакан высотой не менее 10 см, затем влейте в него с помощью пипетки или коктейльной соломинки спирт, смешанный с водой (не менее 70 % спирта), предварительно его подкрасив. Маленьким каплям потребуется несколько секунд, чтобы достичь дна, более крупным – чуть меньше секунды, но вам хватит времени, чтобы проследить за ними. Как заметил Плато, вы получите довольно большие капли (диаметром около сантиметра) сферической формы, в то время как капли воды того же размера в воздухе оказались бы сильно деформированными силой тяжести. Это и неудивительно: если ввести характеризующую такие капли капиллярную длину, определяемую формулой (1), то в знаменателе последней для капли, пребывающей в масле, следует заменить плотность воды на разницу плотностей спиртового раствора и масла. Понятно, что такая капиллярная длина окажется намного больше, чем вычисленная для воды. Кроме того, вы можете оценить и скорость падения капель. Сравните ее с величиной, полученной по формуле Стокса, о которой мы поговорим в главе 15, «Движение пузырьков и турбулентность».