Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

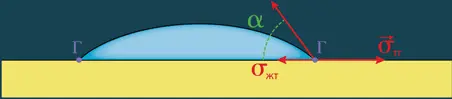
Капля жидкости частично смачивает твердую поверхность

На общей для всех трех сред границе Γ на единицу ее длины действуют три силы: две из них, σ жт и σ тг , параллельны поверхности, третья, σ жг , направлена по касательной к поверхности капли (все они обозначены на иллюстрации красным цветом). Граница Γ должна оставаться на поверхности опоры. Поэтому для равновесия достаточно, чтобы сумма проекций сил на плоскость опоры была равна нулю, то есть:

σ тг = σ жг cos α + σ жт .

Это так называемое уравнение Дюпре – Юнга. Косинус угла контакта может изменяться от 1 до –1, что соответствует условию – σ жг < σ тг – σ жт < σ жг . При выполнении этого условия говорят, что имеет место частичное смачивание . Капля при этом образует сферический купол.

В случае когда σ тг – σ жт > σ жг , капля растекается до тех пор, пока это возможно, образуя при этом очень тонкую пленку. Это так называемый случай полного смачивания .

Если же σ тг < σ жт – σ жг , то капля отделяется от опоры, не смачивая ее совсем. Возможно, читателю приходилось видеть капельки ртути на столе около разбитого термометра (см. илл.) или скатывающиеся по перьям утки капельки воды – это примеры отсутствия смачивания.

Капли ртути не смачивают поверхность. Маленькие капли имеют четкую сферическую форму, большие – сплющены силой тяжести

Однако одного этого соотношения оказывается недостаточно для описания геометрической формы обоих пузырьков и границы между ними.

Недостающее геометрическое соотношение можно вывести, если вспомнить, что силы поверхностного натяжения, действующие в любой точке A окружности Γ, ограничивающей поверхность, должны уравновешивать друг друга (то есть их векторная сумма должна быть равна нулю). Этих сил всего три, каждая направлена по касательной к одной из сфер (1, 2 или 3), и они стремятся сжать соответствующие шаровые сегменты. Все три силы равны по модулю (который составляет отношение σ’ к единице длины). Таким образом, для достижения равновесия они должны попарно составлять между собой углы в 120° (илл. 8). Аналогичное рассуждение позволяет определить и форму капли на твердой плоскости (см. главу 6, врезку «Капля на поверхности»).

Пена образуется из очень большого количества пузырьков, однако ее структура определяется из тех же условий, которые мы использовали выше для двух пузырей.

8. Мыльные пузыри на плоской поверхности. Углы, образованные стенками, соединяющими между собой три пузырька, составляют 120°. В плотной пене шесть разделяющих плоскостей между четырьмя соприкасающимися пузырьками обладают симметрией тетраэдра: они образуют углы в 109,5°

Необычные формы, которые могут принимать мыльные пузыри, далеко не ограничиваются одной сферой. Если мыльная пленка не свободна, а натянута на некоторую рамку, то она порой образует удивительные, кажущиеся невозможными фигуры! Давайте начнем с погружения двух одинаковых колец в мыльную воду. Приложив толику усердия и аккуратности, мы можем получить пузырь в форме цилиндра, накрытый с обеих сторон сферическими «шапками» (илл. 9). Перепад давления Δ P внутри и снаружи пузыря связан с радиусом цилиндра R по формуле, аналогичной формуле Лапласа, но без коэффициента 2:

Δ P = σ’/ R . (3)

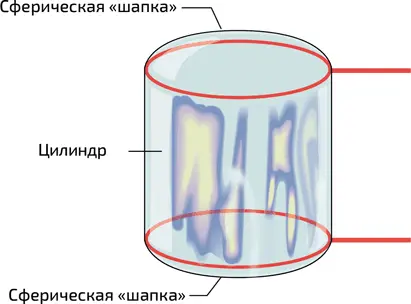
9. Цилиндрический мыльный пузырь, сформировавшийся между двумя кольцами. Две сферические «шапки» замыкают пузырь

«Шапки» пузыря при этом являются сферическими сегментами радиуса 2 R, который определяется формулами (2) и (3). А что произойдет, если они лопнут? При этом исчезнет перепад давления внутри и снаружи мыльной пленки. В результате пленка между двумя кольцами, для того чтобы минимизировать поверхностную энергию, перестает быть цилиндрической и деформируется (илл. 10). Получающаяся в результате такой деформации поверхность приобретает форму лошадиного седла и называется катеноидом. С математической точки зрения это поверхность, которая формируется вращением цепной линии вокруг оси (цепная линия, в свою очередь, – это кривая такой формы, какую принимает подвешенная между двумя точками цепочка, например колье). При изменении формы рамки, независимо от ее геометрии, поверхность, принимаемая пленкой, всегда будет соответствовать минимуму ее площади (такая поверхность называется минимальной) (см. главу 6, врезку «Кривизна, средняя кривизна, цепочка и катеноид»).