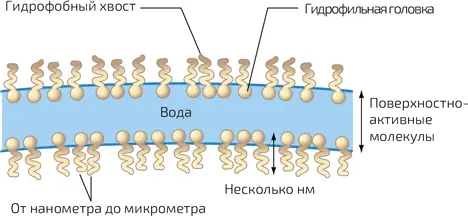
5. Схема мыльной пленки. Молекулы поверхностно-активного вещества уменьшают поверхностное натяжение воды и тем самым препятствуют уничтожению мыльного пузыря. Гидрофильная головка обычно обладает электрическим зарядом и поэтому сильнее взаимодействует с молекулой воды, которая обладает электрическим дипольным моментом (см. главу 16, илл. 5)
Формула Лапласа
Откуда же берется избыточное давление Δ P , отличающее давление внутри мыльного пузыря от атмосферного? Для сферического мыльного пузыря радиусом R расчет прост. Поверхностная энергия равна произведению площади поверхности на поверхностное натяжение: S σ’ = 4π R 2σ’, где σ’ = 2σ, то есть вдвое превышает поверхностное натяжение мыльной жидкости, так как пленка имеет две стороны. Небольшое увеличение радиуса пузырька δ R приводит к изменению поверхности на величину 8π R δ R и, следовательно, к изменению энергии поверхности на 8πσ’ R δ R (илл. 6). Это изменение энергии должно компенсироваться работой сил давления, приложенных к стенкам пузырька при увеличении его радиуса (работа силы равна энергии, переданной системе этой силой в процессе перемещения). Эта работа равна избыточному давлению Δ P , умноженному на изменение объема пузыря, то есть 4π R 2δ R Δ P . Поэтому мыльный пузырь радиусом R пребывает в равновесии тогда, когда давление воздуха внутри превышает атмосферное на
Δ P = 2σ’ /R. (2)
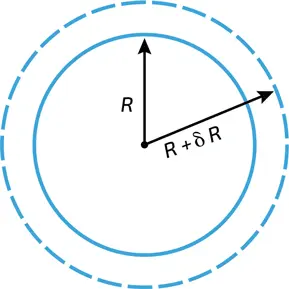
6. Изменение энергии, вызванное бесконечно малым расширением пузырька, должно быть равно нулю в состоянии равновесия
Это соотношение называется формулой Лапласа, в честь физика, который вывел его в 1806 году (см. главу 5, «Высота приливов и их прогнозирование»). Избыточное давление Δ P тем больше, чем меньше пузырь. Вы легко можете проверить его справедливость, соединив два пузырька разного размера тонкой трубочкой: маленький пузырь тут же станет расти, а большой – уменьшаться!
Для миллиметрового пузыря значение избыточного давления составляет порядка одной тысячной от атмосферного. Для пузырька газа в воде σ’ = σ, и избыточное давление оказывается в два раза меньше, чем в мыльном пузыре того же радиуса.
Соприкасающиеся пузыри и пена
Воспользовавшись формулой Лапласа, мы можем предсказать, какую форму примет система из нескольких пузырьков в пене. Рассмотрим два пузыря радиусом R 1 и R 2 соответственно (илл. 7). Избыточное давление внутри каждого из них равно соответственно Δ P 1 = 2σ’/ R 1 и Δ P 2 = 2σ’/ R 2 . Мыльная пленка, разделяющая два этих пузырька, является сферической поверхностью, изгиб которой должен уравнивать разность давлений Δ P 2 и Δ P 1 . Таким образом, радиус R 3 определяется формулой (2), с R = R 3 в знаменателе и Δ P = Δ P 2 – Δ P 1 :
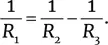
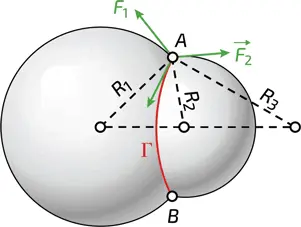
7. Соприкосновение двух пузырей. Плоскости, касательные к поверхностям двух пузырьков, должны иметь между собой и плоскостью, касательной к перегородке Γ, углы 120°, а радиусы пузырьков – удовлетворять соотношению 1/ R 3 = 1/ R 2 –1/ R 1 , где R 2 – радиус меньшего пузыря. В таком случае устанавливается равновесие между воздействующими на поверхность силами поверхностного натяжения F 1 и F 2 и силой поверхностного натяжения, возникающей на внутренней перегородке между пузырьками
Капля на поверхности
Какую форму принимает капля на твердом теле? В отличие от случаев контакта между двумя пузырями, где работает только поверхностное натяжение σ, сегодня ученые различают три типа межповерхностных натяжений: σ жг , σ жт , σ тг , которые соответствуют границам между жидкостью и газом, жидкостью и твердым телом, а также между твердым телом и газом. В зависимости от значений этих трех параметров капля в большей или меньшей степени растекается по поверхности. Степень этого «растекания» измеряется углом α между касательной к поверхности капли и плоскостью, на которой она лежит, в точке их соприкосновения (см. илл.).
Читать дальше
Конец ознакомительного отрывка
Купить книгу



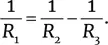




![Лина Сайфер - Театр мыльных пузырей [litres]](/books/434478/lina-sajfer-teatr-mylnyh-puzyrej-litres-thumb.webp)






