Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Таким образом, суммируя все три слагаемых, находим, что масса положительного заряда, движущегося в жидком гелии, составляет 75 m 0 – значение, примерно равное величине, найденной при анализе экспериментов.

В приведенном выше рассуждении мы использовали концепции классической физики, которые без труда описывают движение положительных зарядов. Однако для отрицательных зарядов все оказывается гораздо сложнее…

Мы уже говорили, что жидкий гелий в равновесном состоянии не содержит свободных зарядов. Если ввести в него электрон принудительно, то последний станет причиной локальных потрясений. Чтобы рассказать об этом, сделаем отступление и поговорим об электронной структуре атомов. В квантовом мире существует важный закон: это принцип запрета Паули, который не позволяет находиться в одном и том же квантовом состоянии сразу двум электронам (см. главу 24, «Изотопический эффект и роль кристаллической решетки»). Например, у атома гелия имеются два различных состояния с одной и той же минимальной энергией, которые заняты двумя электронами. Имеются и другие энергетические состояния для электронов, но им соответствуют гораздо более высокие энергии (минимум 20 эВ), и они остаются незаполненными. Таким образом, создать ион He –, добавив в атом гелия третий электрон, оказывается делом невозможным. И все же, будучи разогнанными до сравнительно скромных энергий в 0,5 эВ, электроны проникают в толщу жидкого гелия!

Трое итальянских физиков, Дж. Карери, У. Фазоли и Ф. С. Гаэта, предположили, что при проникновении электрона в объем жидкого гелия последний вовсе не пытается «пристроиться» на свободный энергетический уровень в одном из атомов, «заплатив» за это 20 эВ. Нет, он просто остается самим собой, а окружающие атомы гелия раздвигает, создавая для себя полость и потратив на это всего лишь 0,5 эВ (илл. 3). Образовавшийся «пузырек» и является носителем отрицательного заряда.

Каков же радиус этого пузыря? Его размер обусловлен балансом между силами поверхностного натяжения и давления электрона на поверхность. С одной стороны, образование пузырька требует затратить энергию E 1 , которая тем выше, чем больше объем пузырька (поверхностная энергия, см. главу 6). С другой стороны, электрон в пузырьке непрерывно движется и обладает кинетической энергией E 2 , которая в силу принципа неопределенности тем выше, чем меньше сам пузырек. Радиус R пузырька будет таким, который минимизирует общую энергию E 1 + E 2 . Оценить энергии E 1 и E 2 просто. Первая величина равна E 1 = 4πσ R 2, где σ – известное нам поверхностное натяжение жидкого гелия. Энергию E 2 можно найти из принципа неопределенности (см. главу 22): согласно ему импульс электрона p = m e ν примерно составляет h/ R , поэтому кинетическая энергия E 2 = m e ν 2/2 оказывается порядка h 2/(2 m e R 2), где h – постоянная Планка, m e – масса электрона и ν – его скорость. Минимизируя общую энергию E 1 + E 2 , можно обнаружить, что в состоянии равновесия R 4= h 2/( m e /σ). Точный расчет дает для радиуса пузырька значение R = 2 нм. Собственной массы он практически не имеет, ведь масса электрона пренебрежимо мала по сравнению с присоединенной массой (см. главу 15, «Подъем пузырьков»: δ m = (2/3) πρ R 3, где ρ – плотность жидкого гелия при обычном давлении). Тут нужно заметить, что электрон, подобно иону He +, также поляризует атомы гелия вокруг пузырька, поэтому к δ m следовало бы добавить и массу «свиты», сопровождающей пузырек при его движении в электрическом поле. Однако ввиду его большого по сравнению со снежком радиуса эффект поляризации окружающего гелия слаб и соответствующая масса оказывается пренебрежимо малой по сравнению с присоединенной δ m = 245 m 0 , которая и определяет эффективную массу носителя отрицательного заряда в жидком гелии.

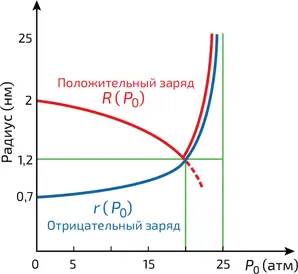
4. Изменение радиуса r носителя положительного заряда («снежка») и радиуса R носителя отрицательного заряда («пузырька») в жидком гелии в зависимости от внешнего давления P 0