Эрик Роджерс - Физика для любознательных. Том 3. Электричество и магнетизм. Атомы и ядра

Предельную точность, нам доступную, можно найти из соотношения λ= h/ mv. Из общей теории распространения волн следует, что если волна проходит через отверстие диаметром, равным λ , или меньше, то она при этом полностью расходится во все стороны; волна же, прошедшая через отверстие диаметром несколько десятков длин волн или еще больше, проходит практически не расходясь (см. гл. 10 ). Если зафиксировать положение движущейся частицы у стенки с точностью до нескольких длин волн λ , то при этом есть риск сообщить ей в поперечном направлении импульс, составляющий большую, но неизвестную часть от его первоначального, направленного вдоль его движения импульса mv . Если же достаточно знать положение частицы грубо, с точностью до нескольких десятков длин волн λ , то за счет такой жертвы ее конечный импульс будет известен с точностью до величины, составляющей малую часть начального импульса.

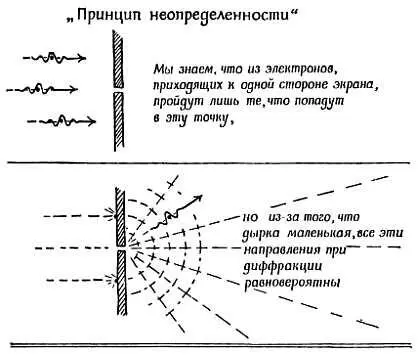
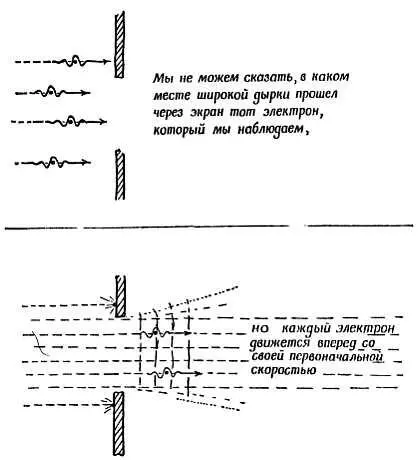
Фиг. 210.

Приводимая ниже таблица содержит утверждения, выглядящие более строгими, чем они есть на самом деле, однако в ней приведены результаты полного исследования с учетом детальной геометрии волн.

Это грубые утверждения относительно точности нашего знания. Однако детальное рассмотрение приводит к тому же самому выводу: в каждом случае произведение неопределенностей равно λ∙mv , т. е. ( h/ mv)∙( mv) = h.

(НЕОПРЕДЕЛЕННОСТЬ КООРДИНАТЫ Δ x)∙(НЕОПРЕДЕЛЕННОСТЬ ИМПУЛЬСА Δ( mv)) ~= (КВАНТОВАЯ ПОСТОЯННАЯ h)

Эти неопределенности отвечают разным измерениям: неопределенность одного измерения приводит к появлению неопределенности в другом. Чем точнее производится одно измерение, тем с меньшей точностью можно предсказать результат другого измерения. Неопределенность возникает не вследствие плохой аппаратуры: она лежит в самой природе. Процесс измерения одной величины обязательно ухудшает возможности точного измерения другой. Так как каждая из этих неопределенностей отражает неточность нашего знания, то последнее обязательно в какой-то степени является неточным. Поэтому не следует говорить, что произведение (Δ x )∙(Δ mv ) точно равно h , скорее следует говорить, что оно примерно равно h или «порядка h ».

Это и есть принцип неопределенности Гейзенберга. Он сыграл исключительно важную роль при построении математического аппарата для описания волн-частиц в атомах. Его строгое толкование в опытах с электронами таково: подобно световым волнам электроны сопротивляются любым попыткам выполнить измерения с предельной точностью. Этот принцип меняет и картину атома Бора. Можно определить точно импульс электрона (а следовательно, и его уровень энергии) на какой-нибудь его орбите, но при этом его местонахождение будет абсолютно неизвестно: ничего нельзя сказать о том, где он находится. Отсюда ясно, что рисовать себе четкую орбиту электрона и помечать его на ней в виде кружочка лишено какого-либо смысла.

Еще более кардинальные изменения вносит принцип неопределенности в философское мировоззрение. Нельзя получить знание с предельной точностью, которую мы желаем, причем дело тут вовсе не в разуме, терпении, технике или деньгах. Мысленно можно построить сверхмикроскоп для наблюдения электрона. Будет ли тогда уверенность, что координаты и импульс электрона одновременно измеримы? Нет. В любом таком микроскопе для наблюдения должен использоваться тот или иной «свет». Вообще, чтобы «увидеть» электрон, в таком сверхмикроскопе на электроне должен рассеяться хотя бы один квант «света». Такое столкновение приводило бы к изменению движения электрона, вызывая непредсказуемое изменение его импульса (комптон-эффект). И для того, чтобы точно определить местоположение электрона, «свет» должен быть исключительно короткой длины волны, иначе его дифракционное изображение размоется. Поэтому этот квант должен быть исключительно коротковолновым, крайне высокочастотным: это должен быть гигантский квант, фотон γ -лучей. Но в таком случае столкновение будет сильным и импульс отдачи электрона окажется весьма неопределенным. Подробные вычисления на основе соответствующих выражений для импульса отдачи в комптон-эффекте и теории дифракции света в микроскопе дают (Δ x)∙(Δ mv) ~= h