Эрик Роджерс - Физика для любознательных. Том 3. Электричество и магнетизм. Атомы и ядра

Атом Бора . Правила

В 1913 г. смелый и неизвестный молодой датский физик Нильс Бор предложил минимальные изменения классической физики, с помощью которых можно объяснить факты и, комбинируя которые, сделать замечательные предсказания. Обратившись к парадоксу со стабильностью атомов, которые должны были бы быстро коллапсировать [190], он предложил следующие новые правила:

ПЕРВОЕ ПРАВИЛО. Атомы построены в соответствии с моделью Резерфорда, но электроны движутся по стабильным орбитам без излучения . (Хотя этим заявлением противоречие было только подтверждено, но его ясное признание уже было большим утешением.)

ВТОРОЕ ПРАВИЛО. Разрешены только некоторые орбиты. Эти стабильные орбиты определяются по квантовым правилам следующим образом. У электрона, движущегося по стабильной орбите, действие должно всегда быть равным h , или 2 h , или 3 h …, n h … [191]. Имеем

ДЕЙСТВИЕ = ЭНЕРГИЯ ∙ ВРЕМЯ,

= [СИЛА ∙ РАССТОЯНИЕ] ∙ ВРЕМЯ,

= [СИЛА ∙ ВРЕМЯ] ∙ РАССТОЯНИЕ,

= ИМПУЛЬС ∙ РАССТОЯНИЕ.

Для круговой орбиты, например, мы смело берем в качестве расстояния длину окружности и пробуем проверить правило:

ИМПУЛЬС ∙ (ДЛИНА ОКРУЖНОСТИ) = h,

или 2 h, или 3 h…

Вообще, mv∙2 π R= n h, где n = 1 соответствует низшей разрешенной орбите, n = 2 — следующей и т. д. Квантовое число n должно быть целым числом.

На модель атома в виде солнечной системы таким образом накладываются жесткие ограничения: разрешены лишь определенные орбиты, а именно только такие, на которых ДЕЙСТВИЕ равно n h , где n — целое число.

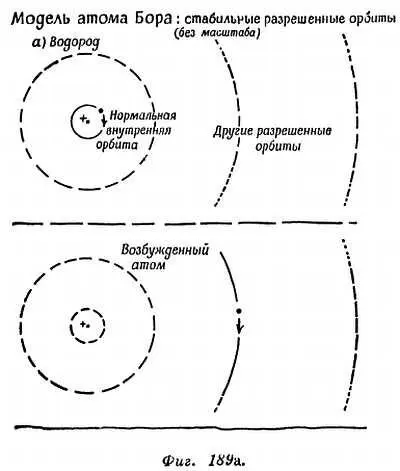
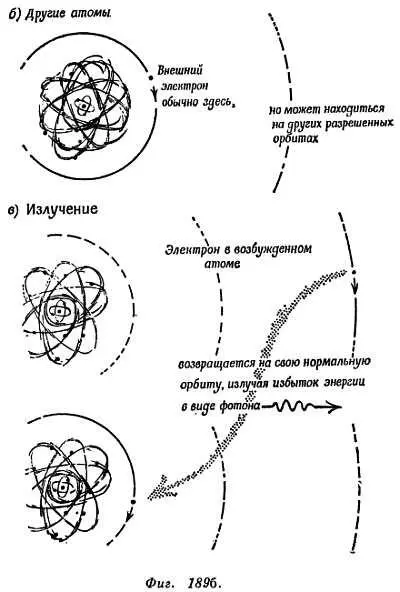
ТРЕТЬЕ ПРАВИЛО. Один из электронов атома можно переместить (например, при бомбардировке) на свободную внешнюю орбиту, так что получится «возбужденный» атом с большей энергией. Затем электрон может перескочить с внешней орбиты на свободную внутреннюю. Когда это происходит, атом испускает избыток энергии в виде кванта света.

h∙ЧАСТОТА ИСПУЩЕННОГО СВЕТА = ИЗБЫТОК ЭНЕРГИИ ЭЛЕКТРОНА=

= ЭНЕРГИЯ ЭЛЕКТРОНА на «внешней» орбите — ЭНЕРГИЯ ЭЛЕКТРОНА на «внутренней» орбите

Атом Бора . Плодотворная теория

Бор сохранил резерфордовскую картину атома, в котором электроны мчатся по орбитам вокруг ядра, притягивающего их с силой, обратно пропорциональной квадрату расстояния. Поэтому «диаграмму холма» для их энергии (диаграмму потенциальной энергии) нужно было бы изображать по-прежнему. Как и в случае настоящей солнечной системы, эта диаграмма для сил притяжения изображает яму вместо холма. Но второе правило квантовых ограничений Бора как бы вырезает уступы вдоль стен ямы и ограничивает орбиты этими уступами. На фиг. 191 показан набросок «диаграммы холма» для Солнца, вокруг которого по круговой орбите движется одна планета, а другая описывает эллипс. Этот «холм» был хорош для сил притяжения к Солнцу.

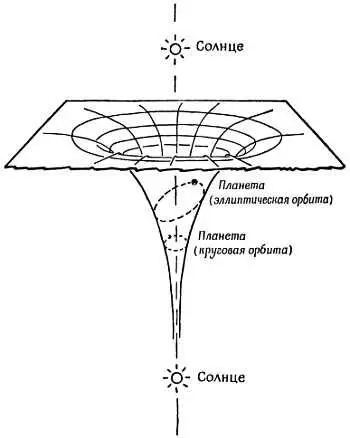
Фиг. 191. Энергетический холм (яма).

Диаграмма для солнечной системы (из книги К. Mendelsshon , What is Atomic Energy, Sigma Books, Ltd.).

Аналогичной была бы «диаграмма холма» для ядра и электронов в «атоме Резерфорда без квантовых ограничений». На фиг. 192 показана упрощенная «диаграмма холма» атома с набором «квантовых уступов» для круговых орбит. В схеме Бора были учтены также другие уступы (уровни энергии), отвечающие эллиптическим орбитам. Форма, размеры и другие характеристики каждой орбиты были определены несколькими квантовыми числами.

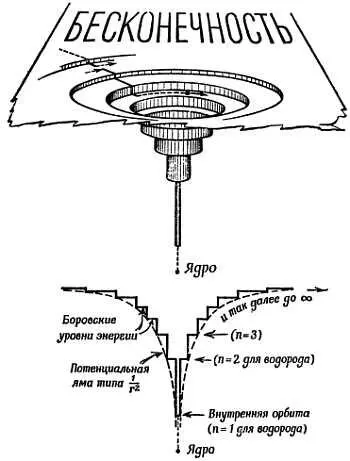
Фиг. 192. Энергетический холм (яма).

Диаграмма для модели атома Бора (из книги К. Mendelsshon , What is Atomic Energy, Sigma Books, Ltd.).

Низший уступ, определенный по квантовым правилам Бора значением n = 1, дает наименьшую разрешенную орбиту. Здесь энергия электрона минимальна; эта орбита наиболее стабильна, поэтому можно было бы ожидать, что электрон будет падать вниз до этого уровня, если только это возможно, и останется здесь. Действительно, следовало бы спросить: почему же не все электроны падают на этот нижний уступ, а все атомы не сжимаются до минимальных размеров? Мы знаем, что так не происходит, и это была одна из многих тайн, которые вскоре объяснились правилом, сформулированным В. Паули под названием принципа исключения [192]. Здесь принцип в сущности утверждает, что на уступе может находиться лишь один электрон, только один электрон с данным набором квантовых чисел. Никогда, ни в каком атоме несколько электронов не могут занимать совершенно одинаковые орбиты. Теперь, правда, мы удваиваем каждый выступ, чтобы поместить туда два электрона с противоположными спинами. С помощью современных знаний можно обосновать принцип Паули, однако долгое время он оставался произвольным, но очень полезным руководством для моделей атома.