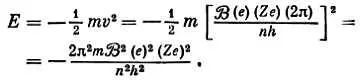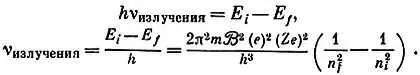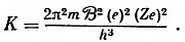Эрик Роджерс - Физика для любознательных. Том 3. Электричество и магнетизм. Атомы и ядра

Сегодня понятие «стабильные орбиты» звучит слишком категорично, но мы будем использовать лишь их существенное свойство — определенность энергии на каждой из них — и поэтому будем говорить об «уровнях энергии».

Так Бор преобразовал спектроскопию, которая была эмпирической схемой исследования газов, в важное средство изучения атомной структуры.

Фиг. 195. Размещение линий спектров по шкале частот.

а— проанализированный по сериям спектр гелия; б— видимые серии атомарного водорода.

Спектроскопическая постоянная по Бору. Примите на веру или вычислите сами

Предсказание постоянной К требует математических выкладок для вычисления энергии электрона в поле ядра. Примите на веру результаты таких выкладок, приведенные на математической схеме (фиг. 196), или проследите за приведенными ниже вычислениями.

Фиг. 196. Схема математических расчетов для атома Бора.

Нам нужно знать энергию электрона для квантовых чисел n = n iи n = n f. Тогда мы сможем предсказать частоту измеряемого фотона, поскольку

h∙ vизлучения = Δ E= Δ E i— Δ E f.

Электрон, движущийся по орбите, имеет энергию Е , складывающуюся из кинетической энергии (К. Э.) и потенциальной энергии (П. Э.) (которая равна энергии, накопленной в электрическом поле системы электрон + ядро). Перенесем электрон из бесконечности на расстояние r от ядра с зарядом Z e . Он притягивается ядром, поэтому при сближении электрона с ядром энергия переходит от электрического поля к электрону (в виде кинетической энергии).

При изменении расстояния х между электроном и ядром на величину d x из электрической потенциальной энергии в кинетическую энергию передается величина

F∙d x, или

Это уменьшение потенциальной энергии атома, т. е. энергия, реализованная из накопленного запаса. (Здесь эта величина положительна, поскольку как F , так и d x отрицательны: F — притяжение внутрь , a d x — смещение внутрь , уменьшение х .) Очевидно, наибольшую потенциальную энергию электрон имел на бесконечности, когда его отвели наиболее далеко от притягивающего ядерного заряда, и он по дороге туда накопил потенциальную энергию. Поэтому, если считать потенциальную энергию электрона на бесконечности равной нулю, то вблизи ядра она должна быть отрицательной.

Потенциальная энергия электрона, перенесенного из бесконечности на орбиту радиусом r , равна

что после интегрирования дает

0 — ∙( e)∙(Z e)/ r

Таким образом, потенциальная энергия электрона равна

П.Э.= — ∙( e)∙(Z e)/ r

Поскольку при орбитальном движении

— mv 2/ r= ∙(- e)∙(Z e)/ r 2 (знак минус показывает направление силы внутрь),

то

П.Э.= — ∙( e)∙(Z e)/ r = — mv 2= — (2 x К.Э.)

Полная энергия

Е= К.Э.+ П.Э.= 1/ 2 mv 2 + (— mv 2) = — 1/ 2 mv 2

Нам нужно знать выражение для энергии Е (через квантовое число n и другие постоянные), не содержащее v или r . Воспользуемся соотношением для орбитального движения

— mv 2/ r= ∙(- e)∙(Z e)/ r 2

и исключим r с помощью квантового правила mv∙2π r= nh:

mv 2 = ∙( e)∙(Z e)/ r

mv = nh/2π r

Разделив первое равенство на второе, получим

v = ∙( e)∙(Z e)∙(2π)/ nh

Тогда

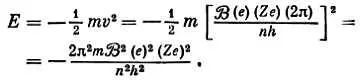
Подставим n = n iдля начального и n = n fдля конечного уровней, между которыми переходит электрон, и получим

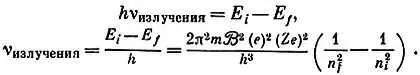
Откуда спектроскопическая постоянная

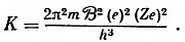
При подстановке измеренных значений е, e / m, h , и для водорода Z = 1 эта формула дает превосходное согласие с величиной K , полученной экспериментально из измерений спектров, а именно 3,286∙10 15в сравнении с 3,290∙10 15.