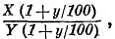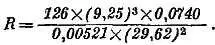Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

1. Какова ошибка в процентах при таком подсчете площади?

2. Вообще если произведение содержит сомножитель X 2, то ошибка х % сомножителя X приводит к ошибке в произведении, равной…%.

3. Если произведение содержит величину X 3, то ошибка х % сомножителя X приводит к ошибке в произведении, равной…%.

4. Если произведение содержит величину X n, то ошибка х % сомножителя X приводит к ошибке в произведении, равной…%.

Задача 4. Ошибки в квадратных корнях

Предположим, что произведение содержит в качестве множителя √ Х .

Как повлияет ошибка в X , равная х %, на точность произведения? Попытайтесь сообразить, какой будет ответ, воспользовавшись одним из следующих способов:

1. Запишите √ Х в виде X 1/2и примите в качестве допущения, что правило решения четвертого вопроса задачи 3 применимо и в том случае, когда n — дробное число.

2. Если множитель √ Х фигурируете произведении дважды, то мы получаем √ Х ∙√ Х , или (√ Х ) 2, т. е. X . Значит, ошибка в X , равная х %, дает ошибку х % в произведении. Поэтому если множитель √ Х встречается только один раз, то мы полагаем, что ошибка составит… %.

…текст не читается…

сталкиваются, например, при разделении изотопов урана для получения атомной энергии. См. задачу в гл. 30 [169].)

Задача 5. Ошибки в делителях

Предположим, нам нужно вычислить частное X / Y . Если значение Y завышено на у %, то как это отразится на частном? Предположим, мы увеличили X на столько же процентов, что и Y . Тогда частное будет, равно

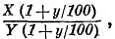
или X / Y , т. е. не изменится. Если знаменатель дроби завышен на у %, то эта ошибка в точности компенсирует ошибку у % в числителе, который тоже завышен. Обе ошибки дают одинаковый по величине и противоположный по знаку вклад в ошибку частного. Следовательно, если завысить на у % знаменатель дроби, то это приведет к такому же результату, как занижение на у % числителя. Значит, ошибка + у % в делителе Y приведена к ошибке частного X / Y , равной — у %. Заметьте, что это следует и из решения четвертого вопроса задачи 3 .

Задача 6. Вычисление результата с несколькими множителями

Предположим, эксперимент приводит к результату

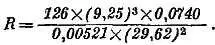
Экспериментаторы дают для своих измерений следующие ошибки в процентах:

от точного значения 126 может отличаться на ±1 %,

9,25 — на ±0,2 %,

0,0740 — на ±0,1 %,

29,62 — на ±0,2 %,

0,00521 — на ±0,1 %.

Если бы все результаты отдельных измерений были занижены на величину ошибки, то

а) числитель записанной выше дроби R был бы занижен на…?…%,

б) знаменатель дроби R был бы занижен на…?…%;

в) вследствие этого окончательный результат ( R = 1530) был бы за…ен?

на…?…%.

В самом худшем случае все результаты измерений, стоящие в числителе, могут быть занижены на величину ошибки, а все результаты измерений, стоящие в знаменателе, — завышены на величину ошибки;

г) в этом случае результат будет за…ен? на…?…%.

На практике мы рассчитываем, что столь коварного заговора против нас не будет. Тем не менее результат, который получается в последнем случае, может служить серьезным предостережением.

Оценка как единственная возможность

Часто бывает необходимо прикинуть ответ, хотя нет данных для точного расчета или нет ни времени, ни возможностей использовать все данные полностью. Например, при сильном снегопаде в большом городе городские власти хотят знать, сколько человек требуется для уборки снега. Неважно, будет ли это 3219 или 3456 человек: вполне достаточно установить, что требуется 3000–4000 человек. Но эту цифру нужно получить быстро: обсуждать и уточнять, требуется ли 3119 человек или на 100 больше или на 50 меньше, не приходится — задержка повлечет большие затраты времени и денег, а может привести и к серьезной опасности.

Однако уборка снега — старая проблема, где подсчет может базироваться на опыте прошлых лет. Иногда возникают новые проблемы, требующие быстрого ответа, хотя даже исходные данные можно оценить лишь ориентировочно. Например, генерал спрашивает полковника, указывая на карту. «Сколько человек может прокормить этот район в течение месяца?» Генерала устраивает незамедлительный, пусть ненадежный ответ: «Около 7000».