Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Ученые установили, что в механике такой неизменной характеристикой является масса: масса сохраняется, говорят они. В течение столетий считали, что вещество неразрушимо и что химические превращения представляют собой лишь обмен частицами вещества.

Тщательное взвешивание химических веществ в колбе до и после химических реакций не обнаружило измеримых изменений общей массы; поэтому ученые выдвинули утверждение о сохранении массы (которое, как они считали, означает сохранение вещества) в качестве универсального правила. Однако этого правила оказалось недостаточно для полного количественного описания столкновений (а в последнее время мы убедились в том, что правило это в его простейшей форме само по себе неверно). В качестве меры движения тела появилось количество движения Mv , когда было установлено, что эта величиа сохраняется. Цепляясь за величину Mv , как за самый надежный ключ к пониманию движения и его измерению, мы по-прежнему рассматриваем сохранение количества движения как прочную основу механики.

Теперь мы располагаем двумя правилами для любой замкнутой [131]системы:

ПРИ ЛЮБОМ ВЗАИМОДЕЙСТВИИ СУММАРНАЯ МАССА МОСТАЕТСЯ НЕИЗМЕННОЙ

(масса М — скаляр ). Это правило называется законом сохранения массы .

ПРИ ЛЮБОМ ВЗАИМОДЕЙСТВИИ СУММАРНОЕ КОЛИЧЕСТВО ДВИЖЕНИЯ MvОСТАЕТСЯ НЕИЗМЕННЫМ

(количество движения — вектор ). Это правило называется законом сохранения количества движения .

Эти правила позволяют нам делать предсказания или извлечь полезные сведения из измерений. Они представляют собой в известном смысле сущность физики и дают возможность привести природу в стройную систему. (Они напоминают правила проверки бухгалтерского баланса, например: итоговая сумма в графе «приход» должна быть равна итоговой сумме в графе «расход».)

Существуют ли другие подобные правила? Сохраняются ли также величины Mv 2, Mv 3и т. д.? Измерения М и v при столкновениях показывают, что величины Mv 3и Mv 4безусловно не сохраняются, поэтому к ним не проявляют интереса и не присваивают им названий. Что же касается величины Mv 2, то она представляет интерес: в некоторых случаях она сохраняется, а в других случаях переходит в иные формы весьма важной и удобной характеристики, которую мы называем энергией . Величине Mv 2, или, вернее, величине 1/ 2 Mv 2! присвоено наименование кинетическая энергия . Мы вернемся к ней в одной из последующих глав.

Изменение количества движения дается произведением ( сила )∙( время ). Мы увидим, что изменение кинетической энергии дается произведением ( сила )∙( расстояние ). Это простое произведение, содержащее силу и размер, и нет ничего удивительного, что величиной 1/ 2 Mv 2удобно пользоваться.

ПРИМЕРЫ ИЗМЕНЕНИЙ КОЛИЧЕСТВА ДВИЖЕНИЯ

Опыт 2.Грубый опыт со столами на колесах. Студенты А и В сидят на двух столах, снабженных колесиками на шарикоподшипниках (роликовых коньках). Оба стола в начальный момент неподвижны и достаточно удалены друг от друга. Студенты тянут за веревку, и столы сближаются (фиг. 198), пока не столкнутся.

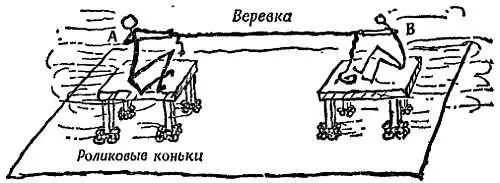
Фиг. 198. Грубый эксперимент.

Если массы (студент + стол) не равны, то туго натянутая веревка сообщает им неодинаковые ускорения. Сближаясь, обе массы приобретают неодинаковые скорости. При столкновении они сводят к нулю количество движения друг друга, и движение прекращается.

Опыт иллюстрирует изменение количества движения, но не дает доказательства его сохранения, если только не измерять приобретаемые количества движения.

Задача 3.

При сближении столов в описанном выше демонстрационном опыте веревка все время туго натянута, ее тянут к себе оба студента или один из них. Предположим, что:

а) студент А крепко держит свой конец веревки, а студент В тянет веревку к себе, поддерживая натяжение постоянным и равным 100 ньютон, или

б) студент В крепко держит свой конец веревки, а студент А тянет веревку к себе, поддерживая натяжение постоянным и равным 100 ньютон, или

в) студенты А и В тянут веревку каждый к себе, поддерживая натяжение постоянным и равным 100 ньютон.

Какие различия вы рассчитываете заметить для этих трех случаев: