Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Задача 2. Столкновение ядер

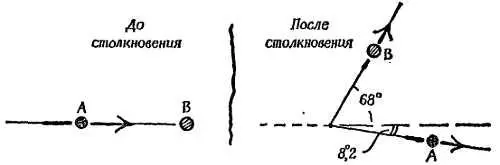
Измерения, выполненные на реальном снимке следов в камере Вильсона, для быстрой альфа-частицы А (ядра гелия), налетающей на неподвижную частицу В (скорости даны в произвольных единицах), позволили получить следующие данные [129]:

До столкновения частица А двигалась со скоростью 2,00 единицы в 1 сек. После столкновения частица А двигалась со скоростью 1,90 единицы в 1 сек в направлении, составляющем 8°,5 с направлением ее первоначальной траектории.

Частица В двигалась после столкновения со скоростью 1,25 единица в 1 сек под углом 68° к направлению первоначальной траектории А (следы обеих частиц образуют Y-образную вилку с углом 76°,5).

Требуется установить природу частицы В , сопоставив ее массу с массой частицы А согласно приведенной ниже методике. Для удобства воспользуемся относительной шкалой атомных масс, принятой в химии, в которой масса ядра гелия А равна 4,0 «атомным единицам массы» (а. е. я,). Тогда, если бы частица В была ядром кислорода, ее масса равнялась бы, 16,0 а. е. м.; в случае азота масса частицы В составляла бы 14,0 а. е. м.; в случае гелия — 4,0 а. е. м., в случае тяжелого водорода — 2,0 а. е. м.; масса ядра обычного водорода равна 1,0 а. е. м.

При определении массы частицы В воспользуйтесь предлагаемым перечнем. (Если у вас получится в ответе какое-нибудь дробное число, например 0,2 или 5,3, то это значит, что вы открыли новую атомную частицу, которую следовало бы как-то назвать в вашу честь.)

а) Начертите на большом листе бумаги в подходящем масштабе векторную диаграмму количеств движения следующим образом: проведите векторы количества движения частицы А до и после столкновения и отметьте количество движения, которое должна приобрести частица В , чтобы в целом количество движения сохранялось.

б) Измерьте вектор количества движения частицы В и, воспользовавшись приведенными данными о скорости, вычислите массу частицы, В .

в) При построении вы, вероятно, воспользовались углом 8,3°, а не 68°. В этом случае измерьте подходящий угол на вашей диаграмме и сравните его с углом 68°. (Получающееся совпадение служит частичной проверкой правил сложения и сохранения количества движения, из которых вы исходили при построении диаграммы.)

Фиг. 197. К задаче 2

г) Если вы знакомы с понятием кинетической энергии тела, которая равна 1/ 2 mv 2(см. гл. 26 [130]), то рассмотрите эту задачу еще раз. Возьмите 4,00 в качестве массы частицы А , а в качестве массы частицы В полученное вами значение и посмотрите, сохраняется ли кинетическая энергия. Если она сохраняется, то взаимодействие представляет собой простое упругое столкновение без каких-либо ядерных превращений. Если же кинетическая энергия не сохраняется, то при взаимодействии должна поглощаться или выделяться ядерная энергия.

Законы сохранения

Что бы ни происходило, количество движения, которое потеряло одно тело, приобретается каким-нибудь другим телом (или телами): векторная сумма количеств движения никогда не меняется .

Чтобы придать этому правилу универсальный характер, необходимо, как мы теперь знаем, учитывать количество движения, уносимое электромагнитными полями, например световыми волнами, и хотя мы по-прежнему вычисляем количество движения в виде произведения ( масса )∙( скорость ), мы учитываем релятивистское свойство массы возрастать по мере ускорения движения.

Релятивистское изменение массы незаметно при обычных скоростях, даже при астрономически больших значениях скорости, но оно приводит к возрастанию массы и количества движения до бесконечно больших значений, когда мы наблюдаем атомные частицы со скоростями, приближающимися к скорости света.

Это простое правило проверки баланса — суммарное Mv после столкновения равно суммарному Mv до столкновения — делает количество движения чрезвычайно важной и удобной для расчетов величиной. Изучение механики движущихся тел, будь то планеты или атомы, похоже на выслеживание банды преступников, которые постоянно меняют свой внешний облик. Сыщик выискивает признаки, которые можно, пользуясь услугами тайных агентов, распознать и проследить при любых изменениях внешнего облика (специфическая форма уха, золотой зуб, хромота и т. д.).