Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

ПРИ ЛЮБОМ ВЗАИМОДЕЙСТВИИ В ЗАМКНУТОЙ СИСТЕМЕ (НА КОТОРУЮ НЕ ДЕЙСТВУЕТ ИЗВНЕ РЕЗУЛЬТИРУЮЩАЯ СИЛА) КОЛИЧЕСТВО ДВИЖЕНИЯ, РАССМАТРИВАЕМОЕ КАК ВЕКТОР, СОХРАНЯЕТСЯ.

Количество движения — вектор

В каждой части соотношения F∙Δ t= Δ( Mv) содержится векторная величина. Сила есть вектор, время же не имеет направления в пространстве — это просто число (скажем, число тиканий часов), которое нужно рассматривать как множитель; скорость — вектор, а масса не имеет направления. Масса — это «скаляр», простое число (вроде числа тележек), которое нужно опять-таки рассматривать как множитель. (Умножение скорости 3 м/сек, направленной на восток , на 2 кг дает 6 кг∙м/сек, направленные на восток .) Поэтому мы предполагаем, что импульс силы F∙Δ t и количество движения М v— векторы; эксперимент это подтверждает. Полная формулировка второго закона Ньютона содержит указание на это обстоятельство: сообщаемое ускорение и, следовательно, производимое изменение количества движения совпадают по направлению с направлением приложенной силы . Это может показаться не очень существенным при лобовых столкновениях, когда все движение происходит по одной прямой, но в случае столкновений, происходящих под другими углами, нужно рассматривать количество движения как вектор. Когда сталкиваются автомобили, движущиеся в разных направлениях, и между ними происходит обмен количеством движения, оказывается, что величины Mv подчиняются правилу сложения векторов. На фиг. 195 показано столкновение автомобиля А , движущегося на восток, с автомобилем В , движущимся на север по обледенелой ровной дороге. После столкновения автомобили будут двигаться под некоторым углом к первоначальным направлениям их движения. При этом они будут обладать количеством движения, которое представляет собой векторную сумму количеств движения обоих автомобилей до столкновения.

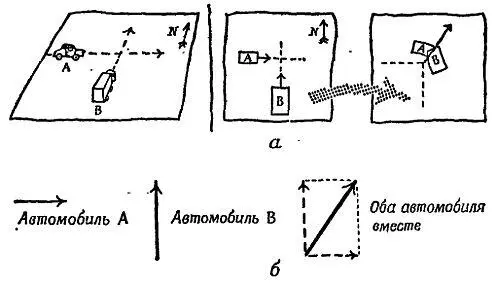
Фиг. 195. Количество, движения как вектор.

а— движение автомобилей до и после столкновения; б— диаграмма векторов количества движения автомобиля А , автомобиля В и обоих автомобилей вместе.

На фиг. 196 показана бомба, скользящая по льду. Бомба разрывается на два осколка, количества движения которых при векторном сложении дают в сумме количество движения бомбы при ее скольжении по льду до взрыва [126].

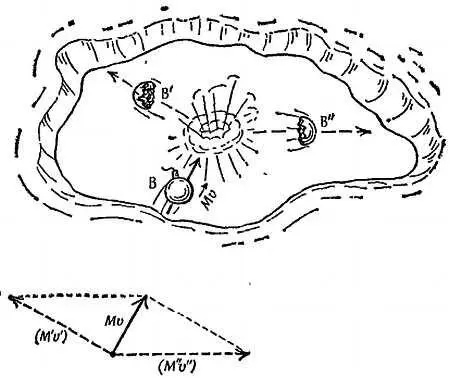
Фиг. 196. Бомба на льду.

Внизу показана векторная сумма количеств движения обоих осколков.

Чтобы проверить векторный характер закона сохранения количества движения, оставим модель железной дороги с вагончиком и будем наблюдать за столкновением брикетов сухого льда на столе, покрытом листом алюминия. Можно также использовать маятники — стальные шары, подвешенные на длинных нитях [127]. В любом случае мы обнаруживаем, что количества движения после столкновения складываются по правилу сложения векторов, и их сумма равна сумме количеств движения до столкновения. Можно поступить и по-другому: проанализировать наши измерения, разложив каждое Mv на компоненты по двум взаимно перпендикулярным направлениям. Если первоначально двигалось лишь одно тело, то целесообразно выбрать ось х в направлении этого движения, а ось у перпендикулярно к оси х , затем можно разложить все количество движения на х - и у -компоненты. Тогда мы обнаружим, что сумма х -компонент после столкновения равна количеству движения до столкновения, а обе у -компоненты после столкновения равны и противоположны друг другу по направлению.

Может показаться, что рисование и анализ траектории сталкивающихся тел в подобных случаях дело надуманное и бесполезное. Но мы умеем фотографировать траектории отдельных атомов и частей атомов, претерпевающих столкновения, анализ же таких траекторий имеет огромное значение в атомной физике. Электроны, заряженные атомы гелия и другие атомные частицы, пролетая через так называемую камеру Вильсона (о ней рассказано в гл. 39 [128]), оставляют отчетливые следы. Если происходит столкновение, то след обнаруживает резкий излом, появляется новый, отходящий в сторону след частицы, испытывающей отдачу, обычно атома газа, в который попала налетающая частица. Зная массы сталкивающихся атомов или атомных частиц, путем построения векторной диаграммы можно извлечь важные сведения о скоростях (количествах движения). Если же известны скорости, то векторная диаграмма позволяет определить отношения масс.