которое, как показано ниже, представляет собой закон F= M∙ a, записанный в иной форме. Попробуем им воспользоваться.
СИЛА∙ВРЕМЯ = Изменение (масса∙скорость),
F∙ t= Δ( Mv).
Тогда
F∙(0,1 сек) = Δ( Mv) = — (10 000 кг х 0) конечное значение Mv — (10 000 кг х 13,2 м/сек) начальное значение Mv
Вот каким образом соотношение F= M∙ aприобретает тот вид, который фактически был дан ему Ньютоном. (Мы предполагаем, что масса М при изменении количества движения остается неизменной.)
Простой вывод
F= M∙ a= M∙( v— v 0)/ t
в соответствии с определением ускорения.
Умножим обе части равенства на t :
F∙ t = M∙( v— v 0) = Mv— Mv 0,
= (Новое значение Mv) — (Старое значение Mv),
поскольку М остается неизменным:
F∙ t = Изменение Mv, т. е. Δ( Mv),
Сжатый вывод
(Здесь мы пользуемся для обозначения длительности действия силы символом Δ t вместо t .)
F= M∙ a= M∙Δ v/Δ t
F∙Δ t= M∙Δ v,
= Δ( Mv)
поскольку М постоянна;
F∙Δ t= Δ( Mv), или изменению величины ( Mv ).
Вывод с использованием математического анализа
F= M∙ a= M∙Δ v/Δ t
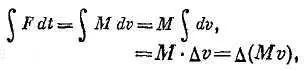
Поскольку М постоянна.
Если F постоянна, то левая часть записывается в виде 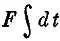 , т. е. F ∙Δ t .
, т. е. F ∙Δ t .
Значит,
F∙Δ t= Δ( Mv)
Если F непостоянна, то , «импульс силы», дает произведение ( среднее значение силы )∙Δ t . Тогда можно записать:
(Среднее значение F)∙Δ t= Δ( Mv).
Если М непостоянна (например, масса ракеты, выбрасывающей в полете продукты сгорания), соотношение F= M∙ aнепригодно, но изменение количества движения Δ( Mv) по-прежнему равно или произведению
(Среднее значение F)∙Δ t
Это возвращает нас к определению силы
F= d( Mv)/d t
т. е. сила равна скорости изменения количества движения. Такова первоначальная формулировка Ньютона, которая справедлива даже в теории относительности.
Проработайте предлагаемую ниже задачу на соотношение
F∙Δ t= Δ( Mv)
Соотношение F∙Δ t= Δ( Mv) представляет собой фактически иную форму записи соотношения F= M∙ a и во многих случаях быстрее приводит к цели. Силы следует выражать в ньютонах. Если воспользоваться этим соотношением для вычисления силы, то ответ автоматически получится в ньютонах.
Задача 1(а)
Человек в течение 1/50 сек прикладывает силу 200 ньютон к летящему футбольному мячу, в котором содержится в общей сложности 0,500 кг материала. Насколько быстрее будет двигаться мяч после такого удара?
Приложенная сила равна ___ ньютон.
Время Δt , в течение которого действует сила, равно ___ сек.
Следовательно, увеличение количества движения должно быть равно ___, ньютон∙сек.
( Примечание . Ньютон∙сек должно быть то же самое, что килограмм∙метр/сек.)
Следовательно, поскольку М = 0,500 кг, увеличение скорости должно быть равно ___ м/сек.
Задача 1(б)
Футболист ударяет по покоящемуся мячу массой 0,5 кг и сообщает ему скорость 14 м/сек. Соприкосновение между ногой и мячом длится 1/ 50ceк. Вычислите силу, действовавшую при этом столкновении.
[Вместо более утомительного способа, которым вы решали задачу 9 в гл. 7 , воспользуйтесь здесь соотношением F∙Δ t= Δ( Mv).]
Изменение количества движения равно ___ кг∙м/сек (или ньютон∙сек). Следовательно, действующая сила должна быть равна ___ ньютон.
Эта же сила в «плохих» единицах равна приблизительно ___ кГ.
Задача 1(в)
Футболист ударяет по мячу массой 1/ 2 кг, летящему на него со скоростью 10 м/сек. Мяч отскакивает назад со скоростью 14 м/сек. Столкновение длится 1/ 50сек. Вычислите среднюю действующую силу. (Скорость и количество движения — векторы. Обратите внимание на употребление знаков плюс и минус.)
Читать дальше

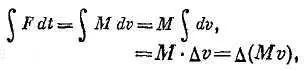
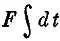 , т. е. F ∙Δ t .
, т. е. F ∙Δ t .










