Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Незадолго до Галилея Стевин показал, что если тело удерживается веревкой в состоянии покоя на наклонной плоскости при отсутствии трения, то к телу приложена сила F :

СИЛА F/ ЗЕМНОЕ ПРИТЯЖЕНИЕ (=ВЕС) = ВЫСОТА НАКЛОННОЙ ПЛОСКОСТИ h/ ДЛИНА НАКЛОННОЙ ПЛОСКОСТИ L

Со стороны наклонной плоскости на тело действует сила Р ; она дается соотношением

P/ W= [ОСНОВАНИЕ НАКЛОННОЙ ПЛОСКОСТИ b] / L

Если трение отсутствует, сила Р должна быть направлена перпендикулярно к поверхности (мы исходили из этого предположения при построении треугольника сил). Если бы сила Р не была перпендикулярна к поверхности опоры, то она имела бы продольную компоненту, увлекающую тело вверх или вниз по наклонной плоскости, т. е. представляла бы собой действие трения [94]. При движении тела до реальной наклонной плоскости всегда имеется трение, препятствующее движению, но здесь мы рассматриваем идеальный случай абсолютно гладкой наклонной плоскости, которая поэтому должна создавать силу реакции, направленную перпендикулярно к поверхности.

Сила реакции Р и сила тяги F в сумме уравновешивают земное притяжение W (фиг. 151)

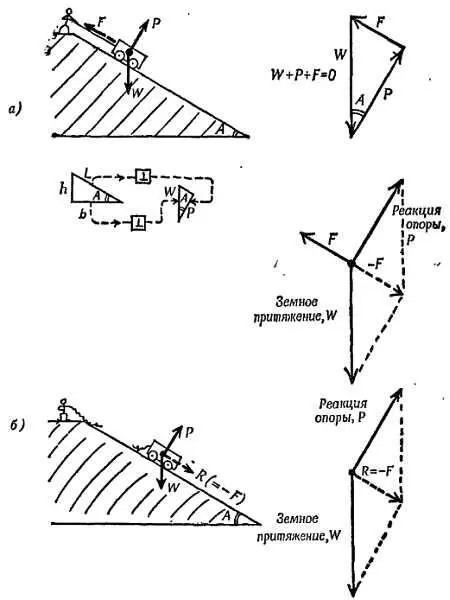
Фиг. 151. Тело на наклонной плоскости.

а— в состоянии покоя; б— движение по наклонной плоскости.

Если перерезать веревку, то тело начнет двигаться с ускорением вниз по наклонной плоскости; мы можем считать, что остальные силы — земное притяжение W и реакция опоры Р — не меняются. В таком случае, если силы W и Р раньше уравновешивали силу F , то их сумма должно быть равна —F , т. е. должна представлять собой силу F, направленную вниз по наклонной плоскости. Таким образом, мы можем считать, что тело, свободно скользящее по наклонной плоскости, ускоряется под действием силы F , направленной вдоль наклонной плоскости и такой, что

F/ W= h/ L, или F= W∙ h/ L

Отношение h / L постоянно по всей наклонной плоскости. Поэтому для любой данной наклонной плоскости сила F одна и та же по всей длине; такие эксперименты, как опыт со скатывающимся колесом, показывают, что эта постоянная сила создает постоянное ускорение, направленное вдоль наклонной плоскости [95]. Если изменить наклон, то изменится сила, действующая на тело вдоль наклонной плоскости, и изменится его ускорение.

Галилей изучал движение тел по различным наклонным плоскостям и пришел к выводу, что их ускорение [96]изменяется прямо пропорционально отношению h / L [97]. В таком случае

УСКОРЕНИЕ, направленное ВДОЛЬ НАКЛОННОЙ ПЛОСКОСТИ = (Постоянная)∙ h/ L

СИЛА F, направленная ВДОЛЬ НАКЛОННОЙ ПЛОСКОСТИ = (Земное притяжение W)∙ h/ L

Итак, ускорение изменяется в такой же пропорции, что и результирующая сила. Таким образом, Галилей создал прочную базу для вывода общего правила

УСКОРЕНИЕ ~ РЕЗУЛЬТИРУЮЩАЯ СИЛА,

которое Ньютон включил в свой второй закон. Это было открытием огромной важности. Еще до Галилея к этому выводу пришли ученые, но он не был ясно сформулирован. Он представляет собой основное соотношение между силой и движением, описывающее движение снарядов, планет, электронов, ракет, поездов, деталей машин и т. д.

Общее соотношение

Многочисленные наблюдения — от приближенных измерений времени, приведенных Галилеем, до косвенных данных из астрономии и современной баллистики — позволяют получить общее соотношение. Если на тело действует постоянная результирующая сила, то тело движется с постоянным ускорением. При удвоении или утроении силы ускорение возрастает в такой же пропорции:

При неизменной массе

УСКОРЕНИЕ ~ СИЛА, или СИЛА ~ УСКОРЕНИЕ.

С другой стороны, чтобы сообщить одно и то же ускорение удвоенной или утроенной массе, необходимо приложить соответственно удвоенную и утроенную силу.

При неизменном ускорении

СИЛА ~ МАССА.

Объединяя оба вывода, можно записать [98]

СИЛА ~ МАССА∙УСКОРЕНИЕ,

F= K∙ M∙ a

Соотношение F= K∙ M∙ a, согласно которому

РЕЗУЛЬТИРУЮЩАЯ СИЛА = (ПОСТОЯННАЯ)∙МАССА∙УСКОРЕНИЕ,

представляет собой обобщенную формулировку, выражающую движение тел с ускорением. Наши демонстрационные опыты не доказывают, что она верна, но они иллюстрируют ее и вносят свою лепту в доказательство ее правильности. Соотношение F= K∙ M∙ a— это наш вариант записи второго закона Ньютона, который мы сформулируем позже. Мы пользуемся этим соотношением для расчета реальных сил: силы реакции пола, которую мы испытываем при прыжке; силы, действующей на автомашину при столкновении; давления газа на стенки сосуда; силы, с которой Земля притягивает Луну. Сначала сделаем несколько замечаний относительно массы и силы (и веса), а потом покажем, как записать соотношение F= K∙ M∙ a в более простой форме, удобной для вычислений.