Однако мы не только можем сделать разность 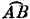 — A ‾ B ‾ пренебрежимо малой — мы можем сделать пренебрежимо малым отношение (разность/хорда) или (
— A ‾ B ‾ пренебрежимо малой — мы можем сделать пренебрежимо малым отношение (разность/хорда) или ( 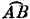 — A ‾ B ‾)/ A ‾ B ‾. Это приводит к тому, что
— A ‾ B ‾)/ A ‾ B ‾. Это приводит к тому, что 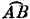 / A ‾ B ‾ становится очень близким к единице. Таким образом, мы можем сказать, что при большом расстоянии между А и В дуга немного больше хорды , при малом расстоянии дуга примерно равна хорде , а при еще меньшем расстоянии дуга почти равна хорде . При сколь угодно малом расстоянии в пределе дуга равна хорде . Математики предпочитают описывать этот предел так: LIm(дуга/хорда) = 1. Теперь мы хотим определить ускорение в некоторый момент времени , когда В и А практически совпадают. Мы не собираемся определять значение этой величины, усредненное по большому расстоянию. Мы хотим знать предел ускорения, когда В совпадает с А . Таким образом, мы говорим: дуга = хорда,
/ A ‾ B ‾ становится очень близким к единице. Таким образом, мы можем сказать, что при большом расстоянии между А и В дуга немного больше хорды , при малом расстоянии дуга примерно равна хорде , а при еще меньшем расстоянии дуга почти равна хорде . При сколь угодно малом расстоянии в пределе дуга равна хорде . Математики предпочитают описывать этот предел так: LIm(дуга/хорда) = 1. Теперь мы хотим определить ускорение в некоторый момент времени , когда В и А практически совпадают. Мы не собираемся определять значение этой величины, усредненное по большому расстоянию. Мы хотим знать предел ускорения, когда В совпадает с А . Таким образом, мы говорим: дуга = хорда, 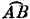 — A ‾ B ‾. Тогда
— A ‾ B ‾. Тогда
Дуга/Δ t= Хорда/Δ t, или 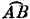 /Δ t = A‾ B‾/Δ tв пределе.
/Δ t = A‾ B‾/Δ tв пределе.
Следовательно,
Ускорение= Δ v/Δ t= ( v/ R)∙ A‾ B‾/Δ t= ( v/ R)∙( v), в пределе ( v/ R)∙ 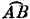 /Δ t
/Δ t
так как 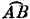 /Δ t есть v . Тогда ускорение Δ v/Δ t= ( v/ R)∙( v) или v 2/ R
/Δ t есть v . Тогда ускорение Δ v/Δ t= ( v/ R)∙( v) или v 2/ R
или ( Скорость на орбите) 2/( Радиус орбиты)
Это соотношение ускорение — v 2/ R очень важно. Мы будем использовать его в теории движения планет, при изучении движения электронов, при изготовлении масс-спектрографов и конструировании циклотронов — везде, где мы сталкиваемся с движением по орбите. Было бы очень важно повторить для себя вывод этого соотношения и поверить в его значение. Поняв, как это делается, вы можете сократить вывод, ограничившись коротким объяснением, двумя эскизами и несколькими алгебраическими выражениями.
Два важных вопроса
Полученный нами результат, ускорение= v 2/ R, вызывает два вопроса:
1. Каким образом может движущееся тело иметь ускорение, но не двигаться быстрее или же не перемещаться к центру круга?
2. Не нужна ли сила для ускорения тела в направлении его движения в соответствии с соотношением F= M∙ a. He действует t ли на массу М , движущуюся по окружности, сила М∙ v 2/ R .
Оба эти вопроса являются выражением тех, реальных трудностей, которые возникли сразу же, как только люди оказались перед необходимостью объяснить движение планет по орбитам. Ответ на вопрос 2 следует из эксперимента: «Да, каждое реальное движение по окружности требует наличия реальной силы, направленной внутрь, a М∙ v 2/ R есть величина этой силы». Чтобы тело могло двигаться по окружности, на него должна действовать сила, направленная к центру. Такая сила может осуществляться с помощью какого-либо реального внешнего воздействия — веревки, пружины или силы тяготения [82] Люди иногда думают, что движение по окружности создает направленную вовнутрь силу, необходимую для поддержания его. Ребенок, который хочет получить леденец, не думает, что от его желания появятся деньги на покупку леденца. Какой-то внешний агент в образе доброго дяди может обеспечить деньги для этой покупки, иначе леденца не будет. Условие движения по окружности аналогично по смыслу. Реальное внешнее воздействие должно обеспечить надлежащую силу, иначе не получится круговой орбиты.
.
Пример А
Вращайте камень, привязанный к веревке (фиг. 107). Вы тянете за веревку, а веревка тянет камень к центру. Веревка буксирует камень и сообщает ему некоторое количество движения в новом направлении.
Представим себе, что веревка делает серию слабых рывков; рывок — и скорость изменила свое направление, еще рывок — снова изменение, еще, еще и так вдоль всей окружности. Если вы отпустите веревку, рывки прекратятся, прекратится и изменение скорости, а камень будет продолжать двигаться по касательной. (Сказать, что «камень улетает по касательной» — значит ввести в заблуждение).
Читать дальше

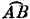 — A ‾ B ‾ пренебрежимо малой — мы можем сделать пренебрежимо малым отношение (разность/хорда) или (
— A ‾ B ‾ пренебрежимо малой — мы можем сделать пренебрежимо малым отношение (разность/хорда) или ( 






![Йэн Стюарт - Математика космоса [Как современная наука расшифровывает Вселенную]](/books/429584/jen-styuart-matematika-kosmosa-kak-sovremennaya-nau-thumb.webp)



