Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

Разобраться в этом было непосильной задачей для всех, кроме Ньютона.

Задача потребовала ясной формулировки законов движения и искусного математического аппарата. Ньютон не только решил эту задачу, но и превратил это решение в основу хорошей теории.

Прежде чем изучать его работы, следует распространить обсуждение вопроса о силе и движении на случай новых сил, искривляющих траекторию движущихся тел. Вы уже встречались с аналогичной ситуацией при рассмотрении полета снарядов, когда вследствие силы тяжести к горизонтальному движению добавляется вертикальная составляющая и в результате траектория становится криволинейной. Это ускоренное движение кажется более легким для понимания. Осмелимся сказать: «кажется более естественным», нежели равномерное движение по круговой орбите с постоянной скоростью.

Фиг. 100.

Ускорение тела, движущегося по окружности

Рассмотрим планету, движущуюся по окружности (камень на веревке, или самолет, или атом, фиг. 101). Будут ли они иметь ускорение? Если нет, то нам трудно будет отыскать действующую на них результирующую силу, но тогда почему они не движутся вперед по прямой? Так все же не имеет ли планета ускорения' Конечно, ускорение вдоль направления ее движения отсутствует, ведь мы выбрали случай движения с постоянной скоростью. Может быть, имеется ускорение, направленное поперек движения планеты, перпендикулярно ему?

Попытаемся нарисовать векторы, с помощью которых можно было бы рассмотреть изменение (вектора) скорости. Пусть тело Р перемещается по окружности радиусом R с постоянной скоростью v , представляющей абсолютную величину вектора скорости тела Р . Направление скорости совпадает с направлением перемещения тела в каждый момент времени. В точке А вектор скорости тела v направлен, как это показано на фиг. 102, по касательной. Если тело движется с постоянной скоростью, то в точках А и В величина вектора скорости v будет одной и той же, но направление будет различным, оба вектора не идентичны. Между точками А и В происходит изменение скорости. (А вследствие этого и ускорение, а поэтому… продолжая эти рассуждения, мы доберемся до планетной астрономии.) Для определения «ускорения» рассчитаем изменение скорости и поделим его на соответствующий интервал времени. Такая процедура предусматривает вычитание векторов для нахождения изменения скорости, что уже было сделано в задаче 1 в начале этой главы.

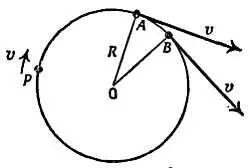
Фиг. 102. Векторы скорости.

Вывод формулы а = v 2/ R .

По мере движения тело Р изменяет свою скорость от ( vвдоль АТ ) до ( v вдоль BT '). Для определения изменения скорости построим векторную диаграмму. Перенесем эти два вектора в общую точку X и проведем линию XY , представляющую вектор скорости vв точке А , и линию XZ , представляющую вектор скорости vв точке В .

Тогда XY будет «старая скорость», a XZ — «новая скорость». Каково же изменение скорости? Какой вектор следует добавить к старому вектору скорости для получения нового вектора скорости?

Такое изменение показано с помощью отрезка YZ , представляющего собой вектор и обозначенного Δ v на фиг. 103.

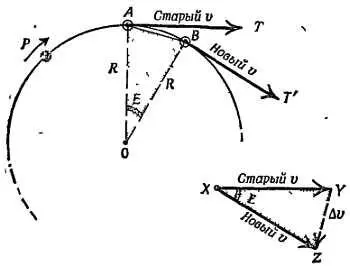
Фиг. 103. Изменение скорости.

Скорости направлены по касательным, перпендикулярным радиусам, поэтому треугольник ОАВ подобен угольнику XYZ векторной диаграммы

Тогда ( Старый вектор v) + Δ v путем сложения векторов дает ( Новый вектор v).

Чтобы увидеть, куда направлен вектор Δ v , изобразим заново первоначальный рисунок, но таким образом, чтобы векторы v сместились вдоль своих направлений до совмещения их точек приложения в точке С (фиг. 104).

Фиг. 104. Направление изменения скорости.

Тогда мы можем рассматривать точку С в качестве X , провести из этой точки старый вектор vи новый вектор vи провести также вектор Δ v . Вектор Δ vпараллелен линии СО , проведенной из точки С в центр круга О . Если поместить точку В очень близко к А , то Δ vбудет направлен по радиусу от АВ к центру. Вектор Δ v— это вектор скорости, направленный к центру круга.