Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

Механизмы

1. Рычаг или детские качели . Детские качели используются и как игрушка, и как устройство для уравновешивания сил. Однако при движении они могут передавать и энергию; надавив на один конец, можно заставить другой поднимать груз. Предположим, что машина (потребляющая топливо) прикладывает силу F 1в точке А , а в точке В бруса ABC проходит ось (фиг. 25). Тогда второй конец может поддерживать в точке С более тяжелый груз. По мере того как машина давит на точку А , тяжелый груз в точке С поднимается.

Фиг. 25. Машина поднимает груз при помощи рычага.

Но давайте подсчитаем изменение энергии, которое определяется не просто силой , а произведением силы на расстояние . Пусть конец А опустился на высоту s 1. Передача энергии от машины к механизму в точке А равна при этом F 1∙ s 1. Второй конец С толкает груз с силой F 2, приподнимая его на высоту s 2. Передача энергии от механизма к поднимаемому в точке С грузу равна работе F 2∙ s 2.

Как же сравнить F 1∙ s 1и F 2∙ s 2? Мы покажем, что они равны. Если F 2во много раз больше F 1, то s 2точно во столько же раз меньше s 1. Вот вам доказательство. Если вы еще не знаете правила уравновешенных качелей или рычагов, то их немедленно дают простые опыты.

Опыты

Опыт 1.Брус ABC (фиг. 26) посажен на ось в точке В таким образом, что в ненагруженном состоянии он уравновешен. Грузы же подвешиваются так, как это изображено на рисунке: 4 кГ на расстоянии 3 м от оси уравновешивается грузом на другом конце на расстоянии 2 м.

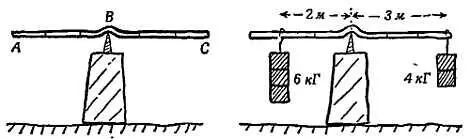
Фиг. 26. Качели для проверки правила равновесия.

Сила∙Плечо = Сила∙Плечо.

Опыт показывает, что правый груз должен весить 6 кГ. В этом примере [140]

4 кГ веса (СИЛА)∙3 м (ПЛЕЧО)= 6 кГ веса (СИЛА)∙2 м (ПЛЕЧО),

причем длина плеча есть расстояние по перпендикуляру между осью и направлением действия силы. Для такого сбалансированного рычага

СИЛА 6 кГ / СИЛА 4 кГ = ПЛЕЧО СИЛЫ 4 кГ / ПЛЕЧО СИЛЫ 6 кГ

Величина груза обратно пропорциональна длине его плеча.

Опыт 2. Более сложный случай.

Вернемся теперь к рычагу, связывающему машину с грузом (фиг. 27).

Фиг. 27. Более сложные случаи уравновешенных рычагов.

В каждом из случаев сумма произведений (со знаками + и —). Сила∙Длина плеча по перпендикуляру от оси до линии силы равна нулю.

Из опыта мы знаем, что силы F 1и F 2 обратно пропорциональны длинам плеч L 1и L 2, т. е. F 2/ F 1= L 1/ L 2. Но из геометрии расстояния s 1и s 2пропорциональны плечам L 1и L 2(треугольники, заштрихованные на фиг. 28, подобны)!

Фиг. 28. Работа машины.

Заштрихованные треугольники подобны. Следовательно, L1/ L2 = s1/ s2. В действительности, нагрузка и усилие перемещаются по дугам окружности, так что s1 и s2 немного искривлены, а «треугольники» на самом деле — секторы. Но к ним применимы те же рассуждения

L1/ L2 = s1/ s2

F 2/ F 1= L 1/ L 2 = s1/ s2

F 1∙ s 1 = F 2∙ s 2

Следовательно, обе передачи энергии, работа F 1∙ s 1и работа F 2∙ s 2равны.

Фиг. 29. Рычаги могут пригодиться.

а— поднятие тяжелого груза, б— согнутый рычаг с одинаковыми плечами.

Работа F 1∙ s 1 — это передача энергии от машины в рычагу, a F 2∙ s 2— передача энергии от рычага к грузу. Поскольку F 1∙ s 1 = F 2∙ s 2, то мы говорим, что рычаг получает и отдает равные количества энергии.

Энергия на входе рычага равна энергии на выходе . Рычаг как механизм просто передает энергию, он не создает и не уничтожает ее. Это, однако, не мешает рычагу быть очень полезным средством для получения нужной величины силы или изменения ее направления, хотя он и не решает проблемы топлива. При наличии же трения в оси возникает небольшая сила сопротивления и некоторое количество вложенной энергии растрачивается бесполезно.

2. Блоки. Колесо блока работает как равноплечий рычаг [141](фиг. 30). Оно изменяет направление силы и зачастую, если мы того хотим, довольно сильно, но если трение отсутствует и колесо идеально круглое, оно не меняет величины силы.