Де Бройлю было 30 лет, когда он нашел свою формулу. Но искать ее он начал за одиннадцать лет до этого — с тех самых пор, как его брат Морис приехал из Брюсселя, где был секретарем первого Сольвеевского конгресса. Того самого конгресса 1911 года, на котором Планк рассказал о развитии «гипотезы квант». Значительность открытий, живые впечатления старшего брата от общения с великими физиками настолько поразили воображение младшего, что он не смог забыть их даже на войне. Постоянное напряжение мысли разрешилось наконец в 1922 году гипотезой о волнах материи. Теперь де Бройль смог дать новое определение понятию «стационарная орбита»: это такая орбита, на которой укладывается целое число «волн электрона» λ .
Если это действительно так, то проблемы устойчивости атома не существует, ибо в стационарном состоянии электрон подобен струне, колеблющейся в вакууме без трения. Такие колебания не затухают, а потому без внешнего воздействия электрон останется в стационарном состоянии навсегда.
Самое трудное — высказать гипотезу. Это всегда процесс нелогический. Но как только гипотеза высказана, строгие законы логики позволяют извлечь из нее все следствия. Главное из них очевидно: если «волны материи» существуют, то их можно обнаружить и измерить. Их действительно обнаружили и доказали их реальность с той степенью достоверности, какая вообще доступна в физике. Однако случилось это четыре года спустя; и об этом мы расскажем потом.
Свои формулы де Бройль написал в 1923 году — за два года до работ Гейзенберга и Шредингера. Их простота и прозрачность основной идеи очень напоминали постулаты Бора. И точно так же, как постулаты Бора, идеи де Бройля еще не были теорией атома — для этого их необходимо было записать на языке уравнений. Когда Вернер Гейзенберг создал матричную механику, он тем самым превратил идеи Бора в точные формулы и строгие уравнения.
Идеи де Бройля стали началом волновой механики, которую создал Эрвин Шредингер.
ОПТИКО-МЕХАНИЧЕСКАЯ АНАЛОГИЯ
Сейчас мы должны усвоить несколько новых фактов. Пусть вначале они покажутся не очень простыми — все равно понять их необходимо, если мы не хотим без конца повторять гладкие, обкатанные фразы о «таинственной стране микромира», которые лишь засоряют ум, поскольку на поверку ничего реального не означают.
Говорим ли мы об атомах или о квантах — мы вновь и вновь обращаемся к свойствам светового луча. Это не случайно. По существу, в нем заключена почти вся нынешняя физика. Сейчас мы еще раз — и более пристально — взглянем на его свойства. Для этого нам нужно возвратиться к Исааку Ньютону и вспомнить смысл его спора с Христианом Гюйгенсом о природе светового луча.
Всегда, во все времена все знали, что луч света в пустоте распространяется прямолинейно; это знание человек приобретает в детстве без всякой науки и физических приборов — после того, как несколько раз ушибется об угол стола. Впоследствии это знание помогает ему избегать многих других опасностей, и постепенно он убеждается в его истинности. Чтобы сделать явление распространения луча более наглядным, в учебниках обычно соединяют источник света и глаз наблюдателя прямой линией, то есть рисуют воображаемую траекторию светового луча .
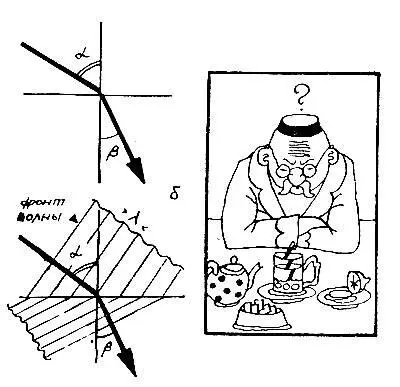
Траектория светового луча
И по смыслу, и по возникающим образам траектория светового луча ничем не отличается от траектории движения частицы. На этом основании во времена Ньютона луч света представляли себе как поток очень маленьких частиц. Конечно, путь этих «световых частиц» (как и путь обычных частиц) может искривляться, допустим, при переходе из воздуха в воду, но понятие траектории ив этом случае сохраняется. В повседневной жизни это понятие очень полезно и не приводит к недоразумениям: оно помогает избегать автомобилей на улицах, определять положение звезд на небе и конструировать фотоаппараты.
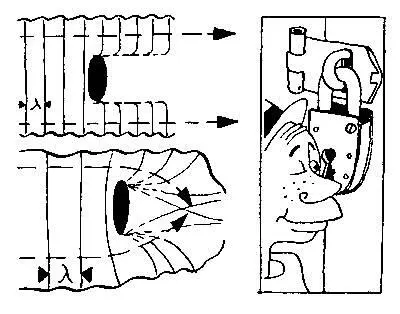
Оптико-механическая аналогия
С развитием экспериментальной физики люди раздвинули узкие границы повседневного опыта и обнаружили новые свойства светового луча: оказывается, он нацело теряет свои привычные свойства, если огибает «очень маленькое препятствие». Физика — наука количественная, и в ней такое неопределенное утверждение не имеет смысла. Маленькое — по сравнению с чем?
Читать дальше













