Марио Бертолотти - История лазера

Однажды Штерн пришел к нему и сказал: «С помощью магнитных экспериментов мы можем сделать еще кое-что. Знаешь ли ты, что существует направленное (пространственное) квантование?» «Нет, ничего не знаю» — ответил Герлах. В то время многие физики не верили, что пространственное квантование действительно существует, и полагали, что это лишь способ выполнения расчетов. Герлах позднее вспоминал, что Петер Дебай заметил ему: «Неужели вы верите, что пространственая ориентация имеет какой-либо физический смысл; это просто указание, как проводить вычисления». Даже Борн придерживался такого же мнения. Штерн, напротив, верил, что это реальный факт и после объяснения этого эффекта сказал Герлаху: «Это стоит попробовать» и предложил: «Почему бы нам не попробовать? Давай проверим это».

Оригинальное предложение Штерна было детально изложено в статье «Метод экспериментальной проверки квантования по направлению в магнитном поле».

«в квантовой теории магнетизма и эффекта Зеемана предполагается, что вектор углового момента атома может принимать по отношению к направлению магнитного поля H только дискретные и хорошо определенные углы, такие, что угловой момент в направлении Я будет целым числом H/2π ».

Чтобы понять это утверждение, необходимо помнить, что уже А. М. Ампер (1775-1836), французский физик, который заложил математические основы электромагнетизма, установив связь между электричеством и магнетизмом, и который за свои таланты был назначен Наполеоном (1808 г.) генеральным инспектором новой системы университетов во Франции, продемонстрировал, что электрический ток в цепи генерирует небольшой магнитный момент, такой, как если бы эта цепь была элементарным магнитом. В атомах орбиты электронов, вращающихся вокруг ядер, могут уподобляться маленьким катушкам, через которые проходит ток. Квантовая механика Бора, улучшенная Зоммерфельдом, позволяет рассчитать магнитные моменты, связанные с каждой орбитой. Эти величины получаются по сложным правилам, найденным Зоммерфельдом. Таким образом, атомы обладают магнитным моментом и ведут себя подобно стрелке компаса, которая ориентируется во внешнем магнитном поле. Если атом помещен во внешнем магнитном поле, его момент, обозначаемый буквой l , будет выстраиваться параллельно внешнему полю согласно правилам электромагнетизма и классической механики. Чтобы сделать это, он будет описывать конус с осью вдоль направления поля (прецессионное движение). Его проекцию на направление поля (будем обозначать ее m) называют моментом вдоль поля (рис. 29).

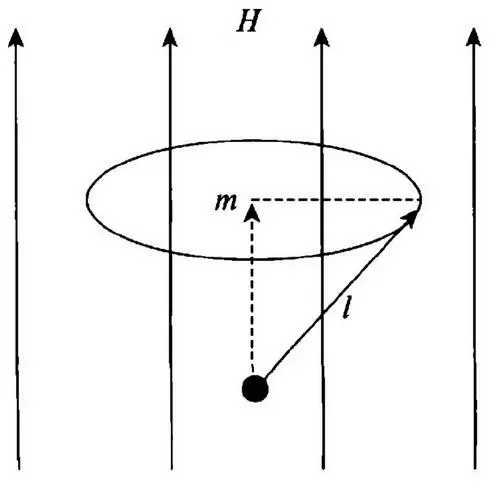
Рис. 29. Прецессия углового момента l в магнитном поле H. Показана проекция m вектора I на H

Теперь получается следующее. Согласно классической механике т компонента вдоль поля может иметь любое возможное значение между + l и — l (т.е. возможен любой угол между l и полем). Но согласно квантовой теории возможны лишь дискретные значения m, соответствующие m = l , ( l — 1), ( l — 2), ..., — l (т.е. разрешены лишь некоторые углы l по отношению к полю) (рис. 30). Согласно квантовой механике величина вектора l равна √( l +1), которая больше, чем максимальное значение m. Поэтому ясно, что l никогда не может точно направлено по полю (заключение, которое глубоко связано с принципом неопределенности Гейзенберга). Чтобы прояснить это для простейшего случая, когда магнитный момент атома (в соответствующих единицах измерения) l = 1/2, вообразим, что магнитное поле направлено снизу вверх, как показано на рис. 31, а атом является человеком, держащим стрелу (которая и есть на нашем рисунке магнитным моментом). В то время, как согласно классическим законам, человек может ориентировать стрелу в любом направлении, согласно квантовой механике позволены только две позиции, показанные на рисунке (мы будем называть их параллельной и антипараллельной ориентацией по отношению к полю), в которых проекция стрелы на направление поля есть либо + 1/2, либо — 1/2 (рис. 31, а). Поэтому длина стрелы √(3/2).

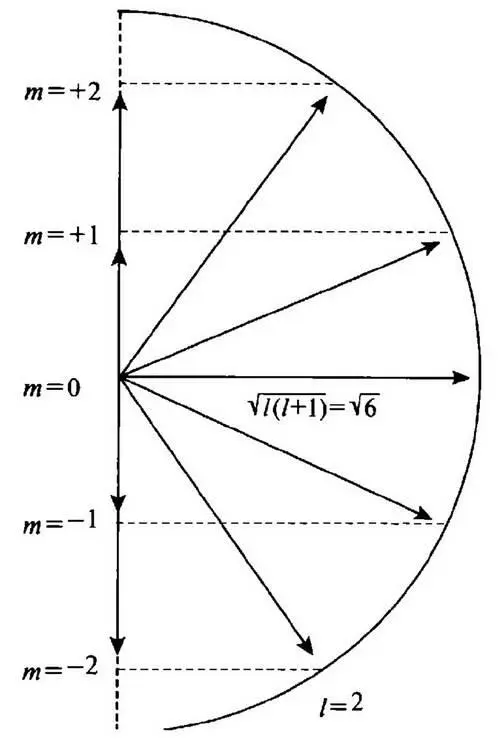
Рис. 30. Показаны возможные ориентации углового момента l на направление внешнего магнитного поля H. На рисунке l = 2 (в соответствующих ед.), а соответствующие ему значения m составляют +2, ±1 и 0. Эти возможные ориентации l показаны стрелками