Марио Бертолотти - История лазера

Эйнштейн рассматривал молекулы, заключенные в сосуде. Согласно постулатам Бора, разработанным к тому времени, каждая молекула может иметь лишь дискретный набор состояний с определенными энергиями. Если большое число таких молекул составляют газ при некоторой температуре, то вероятность одной молекулы находиться в определенном состоянии можно установить, применяя законы статистической механики, установленные Гиббсом, Максвеллом и Больцманом. Эйнштейн предположил, что молекулы обмениваются энергией с излучением, которое присутствует в объеме за счет трех процессов.

Первый процесс, который мы сегодня называем «спонтанным излучением», происходит, если молекула находится не в низшем состоянии энергии, а в некотором высшем состоянии. Тогда она будет переходить в состояние с низкой энергией, испуская фотон с энергией, которая точно равна разности энергий этих двух состояний (рис. 22, а). Этот процесс девозбуждения является процессом, описываемым Бором для молекулы или возбужденного атома скачком переходить в состояние с низшей энергией. Эйнштейн предположил, что этот процесс происходит случайным образом, подобным тому, как радиоактивный атом распадается во времени.

Второй процесс может рассматриваться как обратный первому и является процессом поглощения. Молекула, находящаяся в определенном состоянии энергии, может перейти в более высокое состояние, если ударится с фотоном, имеющим энергию, как раз равную разности между двумя состояниями (рис. 22, б). Этот процесс также рассмотрен Бором. В этом случае фотон исчезает (поглощается) и молекула получает всю его энергию, чтобы перейти на высшее энергетическое состояние.

Третий процесс был впервые введен Эйнштейном и сегодня называется «вынужденным (индуцированным) излучением». Согласно этому процессу, если молекула находится в высшем энергетическом состоянии и с ней сталкивается фотон с энергией, в точности равной разности между состояниями, то она может перейти в низшее состояние. При этом молекула испускает фотон с той же самой энергией, а первый фотон продолжает свое движение свободно, просто «стимулируя» молекулу девозбудиться (рис. 22, в).

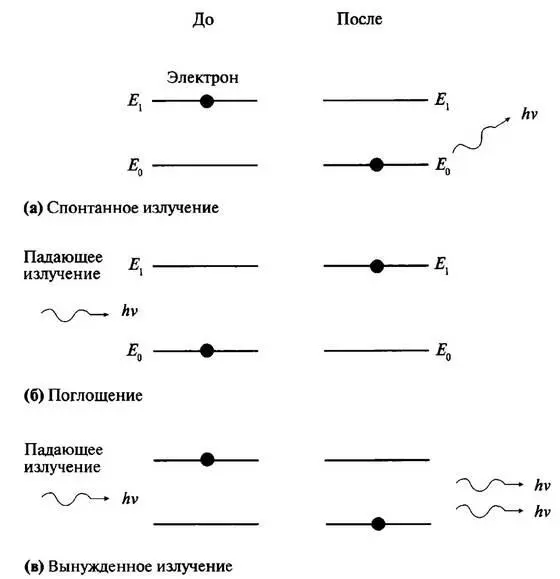
Рис. 22. Верхняя часть (а). Электрон, сидящий на верхнем уровне, спонтанно сваливается на нижний уровень (спонтанное излучение), испуская разность между их энергиями в виде фотона, который испускается случайным образом. На средней части (б) электрон подбрасывается с нижнего уровня на верхний уровень фотоном, который имеет энергию, равную разности энергий этих уровней и которая поглощается (процесс поглощения). Нижняя часть (в). Вынужденное излучение, в результате чего фотон с надлежащей энергией (которая равна разности энергий уровней) ударяет электрон, который сидит на верхнем уровне, вынуждая его спрыгнуть на нижний уровень, испуская при этом другой фотон, идентичный тому, что вызвал этот вынужденный процесс

Если мы теперь предположим, что молекулы могут взаимодействовать с излучением этими тремя процессами и что это взаимодействие не изменяет распределения энергии, которое зависит только от температуры и определяется законом Максвелла—Больцмана, то мы немедленно получаем закон Планка вместе со связанными коэффициентами, которые описывают эти три процесса. Эти коэффициенты сейчас называются коэффициентами Эйнштейна и определяют вероятности переходов. Квантовая теория Бора не дает указаний на законы, управляющие такими переходами, и концепция вероятностей переходов происходит из работы Эйнштейна.

Вывод Эйнштейном закона распределения Планка из введенных коэффициентов вероятности поглощения, спонтанного и вынужденного излучений, позволяет связать эти процессы через эти коэффициенты. Эйнштейну не удалось выразить их через характеристические параметры атома. Такое выражение было получено более чем десятью годами спустя П.А.М. Дираком, который использовал в то время уже полностью разработанную квантовую механику. Однако и выражения, найденные Эйнштейном, устанавливали, что коэффициенты поглощения и вынужденного излучения были равны и что отношение между спонтанным излучением и поглощением обратно пропорционально кубу длины волны. Поскольку вероятность спонтанного излучения можно экспериментально измерить, формулы Эйнштейна могут быть проверены путем сравнения интенсивностей поглощения и спонтанного излучения спектральных линий.