Таким образом, второй закон термодинамики состоит из констатации двух положений — существования и постоянства энтропии в обратимых процессах (Карно) и возрастания энтропии в необратимых процессах (Клаузиус).
Уменьшение энтропии в изолированных системах второй закон запрещает: оно в принципе невозможно: Примеров таких воображаемых невозможных процессов можно привести много: это самопроизвольный переход теплоты от холодного тела с температурой Т 2к более теплому с температурой Т 1> Т 2, например, закипание чайника с водой, поставленного на лед (или замерзание в жару воды в водопроводной трубе). Нетрудно видеть (рис. 3.5), что энтропия при этом уменьшалась бы, поскольку энтропия S воды в чайнике возрастала бы на Q/T 1, а энтропия S льда уменьшалась на Q/T 2. Двигатель, работающий на «концентрации тепловой энергии, отводимой из окружающего пространства» (т. е. производящий работу или электроэнергию из внутренней энергии равновесной окружающей среды) [53] Такой воображаемый ppm-2 иногда называют монотермическим двигателем, так как он должен работать от одного теплоотдатчика с одной температурой To.c. без теплоприемника с более низкой температурой. Отсюда и монотермический — однотепловой («моно» — один).
, относился бы к этой же группе нереализуемых систем. Действительно, получая некоторое количество теплоты Q O.C.от среды при ее температуре T O.C.(а с ней неизбежно и соответствующую энтропию S = Q O.C./T O.C., он выдавал бы некоторую работу, в которой энтропии нет. К чему это привело бы?
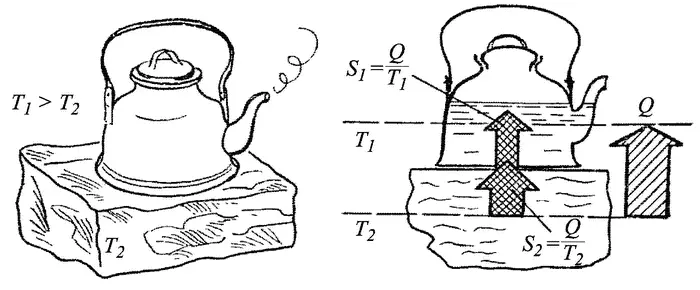
Рис. 3.5. Чайник, кипящий вопреки второму закону термодинамики, но в согласии с первым законом
Если бы вся теплота Q O.C.превратилась в работу, то энтропия исчезла бы совсем. Если же в работу L превратилась бы только часть теплоты Q O.C., а остальную ее часть Q 2двигатель отдал бы обратно, то все равно отданная энтропия была бы меньше, чем полученная так как Q 2< Q O.C.и S 2= Q 2/T O.C.< Q O.C./T O.C.
Чтобы завершить знакомство с энтропией, остается затронуть еще один аспект этой замечательной величины — ее статистическую трактовку. Она была дана двумя великими физиками — Л. Больцманом (1844-1906 гг.) и М. Планком (1858-1947 гг.).
Они подошли к понятию энтропии с другой стороны, так сказать, «изнутри», от молекулярного строения материи. Больцман исследовал законы поведения всего множества молекул, составляющих взаимодействующие части системы, и установил, что существует непосредственная связь энтропии с тем состоянием, в котором эти молекулы находятся.
Каждая молекула обладает в каждый определенный момент определенной энергией, связанной с ее движением и взаимодействием с другими молекулами. Общая внутренняя энергия вещества представляет собой сумму энергий этих частиц. Поскольку молекулы постоянно находятся в хаотическом движении и взаимодействуют между собой, между ними происходит энергетический обмен, приводящий к тому, что энергия все время перераспределяется между ними. Поэтому каждый следующий момент соответствует уже другому микросостоянию системы с другим распределением энергии между молекулами.
Таким образом, микросостояние системы — это такое ее состояние в данный момент, при котором для каждой молекулы определены положение в пространстве и скорость. Это, если так можно выразиться, мгновенный снимок системы.
Изучить в такой ситуации хаоса и беспорядка, существующей в каждом микросостоянии, поведение каждой молекулы, чтобы предсказать ее поведение в дальнейшем, практически невозможно. Но это и не нужно: достаточно знать возможные варианты общего поведения системы, т. е. число всех ее возможных микросостояний.
Число w таких микросостояний может быть очень велико, огромно, но оно все же не бесконечно, так как число молекул конечно, как и число энергетических уровней, на которых они могут находиться.
Но каково же будет состояние системы, определяемое общими характеристиками (плотность, энергия и т. д.), т. е. ее макросостояние в данных условиях? Какое из многочисленных микросостояний она «выберет»? Оказывается, зная число и особенности различных возможных микросостояний, можно установить ее наиболее вероятное макросостояние. Этот закон будет статистическим, что, однако, ничуть не снижает его силы и надежности.
Чтобы показать, на чем он основан, используем наглядный пример, приведенный чл.корр. АН СССР Л.М. Биберманом.
Читать дальше










