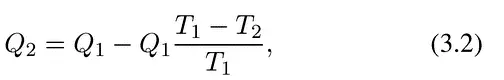Начнем с того, что вернемся к понятию теплорода (у Карно французское слово calorique — «калорик») и представлению о том, как он создает работу (рис. 3.1).
Мы уже говорили о том, что такое понимание связано с теорией о некоем веществе, которое протекает сверху вниз (от высокой температуры к низкой), производя работу; при этом его количество не меняется. С установлением механической теории тепловых явлений это представление, естественно, отпало.
Однако оказалось (как это часто бывает), что в представлении о том, что сквозь двигатель проходит поток «чего-то», не меняющего при его работе свое значение, есть некое рациональное зерно.
Действительно, вникнем немного глубже в уравнение, отражающее принцип Карно, установив из него связь количеств теплоты Q 1и Q 2и температур Т 1и Т 2. Для этого преобразуем его. Очевидно (по закону сохранения энергии — первому закону термодинамики), что Q 2= Q 1— L; тогда основное уравнение Карно можно переписать, заменив работу L на ее значение, так:
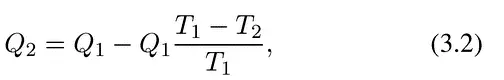
или, после упрощений:
Q 1/T 1= Q 2/T 2(3.3)
Выходит, что отношения количеств теплоты к соответствующим температурам (так сказать, «приведенная» теплота) и на входе теплового потока, и на выходе равны. Значит, действительно, есть тепловая величина, отличающаяся от «просто» теплоты, сохраняющая для двигателя постоянное значение в процессах ее подвода и отвода! [50] Примечательно, что сам С. Карно в определенной степени это чувствовал: везде, где он говорил о теплоте (в смысле величины Q), использовалось слово chaleur (тепло), а где о теплороде — другое, уже упоминавшееся нами слово calorique — теплород. То, что это не случайность, видно из того, что такая терминология ни разу не нарушается.
Замечательное свойство величины Q/T сохраняется и в другом, тоже достаточно важном случае.
Мы уже говорили о том, что двигатель, введенный Карно, — идеальный, т. е. работает без потерь. Это означает, что работа, получаемая от него, максимальна при данных Q 1и температурах Т 1и Т 2, т. е. полностью соответствует величине L в формуле (3.1), Если использовать полученную работу, то цикл может быть пущен и в обратную сторону. Понятие о такой обращенной тепловой машине тоже введено С. Карно в его знаменитой книге. При таком «обращении» идеального цикла все количественные соотношения между величинами, определяющими его работу, останутся прежними, только вместо переноса «теплорода» с высокой температуры на низкую будет происходить обратный процесс — перенос его с низкого уровня температуры на высокий. Для этого потребуется ровно столько же работы, сколько ее было получено, и все вернется в исходное состояние. Другими словами, такой цикл обладает свойством обратимости. На рис. 3.2 показаны оба случая с потоками энергии. Потоки энергии показаны в виде полос, ширина которых пропорциональна потоку энергии. Такие графики называются полосовыми. Отношения Q/T в обоих случаях остаются одинаковыми и на входе теплоты, и на ее выходе.
Таким образом, тепловой двигатель превратится в «тепловой насос», перекачивающий «теплород» с низкой температуры на высокую с затратой работы. Поток приведенной теплоты подобно потоку «теплорода» и здесь пройдет неизменным через машину, но не «сверху вниз», как в двигателе, а «снизу вверх», как в насосе. Если бы заснять действие машины на кинопленку, то ее (и машину, и пленку) можно было бы крутить в любом направлении: картина была бы верной во всех случаях.
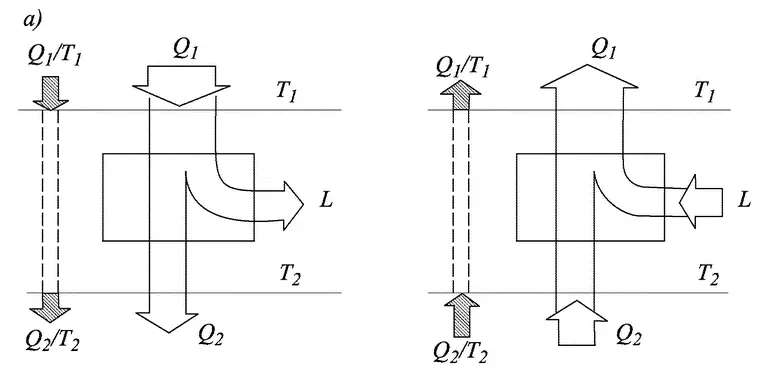
Рис. 3.2. Полосовые графики потоков энергии и энтропии: а — тепловой двигатель; б — тепловой насос
Это замечательное свойство величины Q/T оставаться неизменной при всех идеальных (и, следовательно, обратимых) взаимных превращениях теплоты и работы не могло не обратить на себя внимания.
Р. Клаузиус (1822-1888 гг.) был первым, кто придал величине Q/T самостоятельное значение и ввел ее в науку.
Он назвал ее энтропией. С тех пор (1865 г.) энтропия (ее по стандарту обозначают буквой S) начала свой славный и вместе с тем тернистый путь в науке. Славный потому, что она «работала» и продолжает «работать», помогая решать множество важнейших теоретических и практических проблем (и не только термодинамических). Тернистый потому, что трудно найти другое научное понятие, вокруг которого кипели бы такие страсти и которое вызвало бы столько кривотолков, ошибок и нападок. Достается ей и от идеологов, и от изобретателей ppm-2.
Читать дальше