Впервые правильно поставил и решил эту задачу С. Карно, о котором мы уже писали в связи с первой формулировкой закона сохранения энергии. Со знаменитой книги Карно «О движущей силе огня…» начинается не только история термодинамики, но и вся современная теоретическая теплоэнергетика [46] С. Карно не дожил до признания своих заслуг, и его книга прошла незамеченной. Вторую жизнь дал ей французский ученый и инженер Б. Клапейрон (1799-1864 гг.), издавший книгу Карно в 1834 г. со своими комментариями и дополнениями.
.
По теории теплорода работа паровой машины выглядела очень просто. Теплород от дымовых газов, полученных при сжигании топлива, переходил к воде при высокой температуре, превращая ее в пар. Пар расширялся в цилиндре, производя работу. Затем пар направлялся в конденсатор, где при низкой температуре отдавал теплород охлаждающей воде.
Схема такой машины показана на рис. 3.1, а; поток теплорода Q (ширина полосы соответствует его количеству) «падает» с температуры Т 1на более низкую температуру Т 2< Т 1. При этом производится работа L. Нетрудно видеть, что такое объяснение работы тепловой машины возникло по аналогии с гидравлической машиной (например, водяной мельницей); только роль воды играет «теплород», а напора, обусловленного высотой падения воды Δh = h 1— h 2— разность температур ΔT = T 1—T 2(рис. 3.1, б). Количество воды G, как и количество теплорода Q, не меняется — сколько входит (Q 1), столько и выходит (Q 2). На первых порах такая теория была вполне приемлемой, тем более что из нее следовал правильный и очень важный вывод: тепловая машина может работать только при наличии разности температур. Если ΔT = 0, то теплота будет «мертвой», как «мертвая вода» Леонардо да Винчи при Δh = 0.
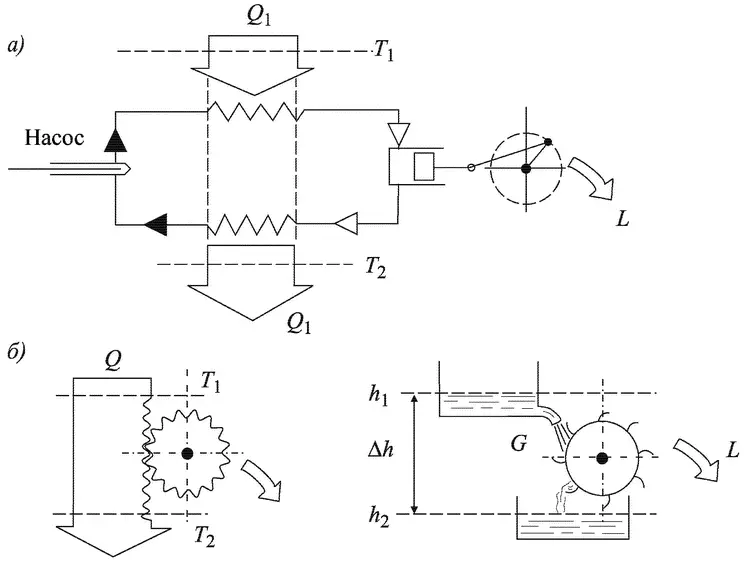
Рис. 3.1. Схема действия паровой машины (двигателя) с позиций теории теплорода: а — «падение теплорода» с температуры Т 1до температуры Т 2, б — механическая и гидравлическая аналогии
У современного читателя, однако, может возникнуть естественный вопрос. Пусть инженеры того времени и не знали закона сохранения энергии, но ведь он все равно действовал! А это означает, что количество отдаваемого внизу при T 2теплорода (т. е. теплоты) должно было быть существенно меньше, чем то, которое поступило наверху при T 1, на количество произведенной работы, т. е. Q 2= Q 1— L.
Как же не заметили этого? Ответ очень прост. Самые лучшие паровые машины того времени имели очень малую эффективность: они превращали в работу не более 3-5% получаемой теплоты. А это означает, что Q 2отличалось от Q 1так, как 95 отличается от 100; но точность тепловых измерений в то время была намного меньше 5%. Поэтому разницу между Q 1и Q 2просто не могли заметить (тем более что никому не приходило в голову, что ее нужно искать).
С. Карно поставил перед собой задачу определить количественно «движущую силу огня», т. е., говоря современным языком, то максимальное количество работы, которое может дать единица количества теплоты.
Несмотря на то, что С. Карно исходил в этой работе еще из теории теплорода, а закон сохранения движущей силы (т. е. энергии) [47] Об этом говорилось в гл. 2.
он сформулировал позже — между 1824 и 1832 гг. — он блестяще решил задачу.
Позднейшим исследователям оставалось лишь придать математическую форму положениям Карно и развить их применительно к новым научным фактам, изложив их с учетом первого закона. Только через четверть века термодинамика пошла дальше, но основные идеи Карно остались незыблемыми. Такая поразительная устойчивость основных положений С. Карно (свойственная вообще великим научным открытиям) связана с тем, что он подошел к задаче с максимально общих позиций, исключив все частности, не имеющие принципиального значения. Он рассматривал не какую-то определенную паровую машину, даже не паровую машину вообще, а абстрактный, идеальный тепловой двигатель, результаты действия которого не зависят от его конструкции. Для этого он ввел специальный цикл, впоследствии названный его именем.
Из многочисленных следствий работы С. Карно для нашей цели — анализа ppm-2 — наиболее важно положение о том, что для непрерывной работы теплового двигателя необходим источник теплоты с более высокой температурой и теплоприемник с более низкой — так называемый принцип Карно. Математическое выражение принципа Карно, определяющее условия перехода теплоты Q в работу L при заданных температурных условиях, было выведено Р. Клаузиусом в виде предельно простой, широко известной формулы
Читать дальше










