Кэйвор и Бэдфорд использовали «кэйворит» для полета на луну. Такой же материал под названием «лунит» был применен коротышками — героями известного романа-сказки Н. Носова «Незнайка на луне», чтобы улететь с луны на землю. Но коротышки пошли еще дальше — нашли другой материал — «антилунит», нейтрализовавший действие первого!
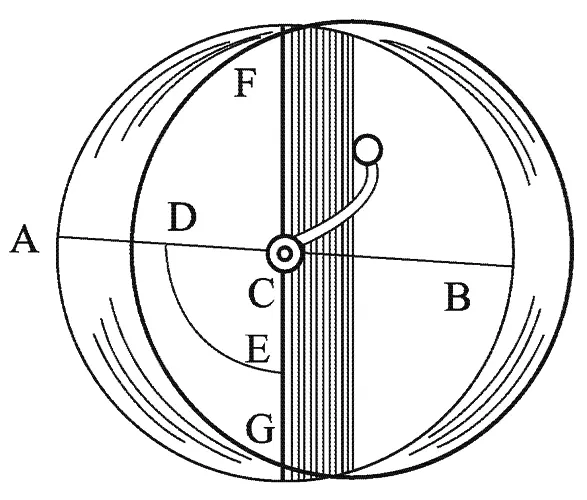
Рис. 1.8. Катящийся вечный двигатель, описанный Д. Борелли
Д. Борелли не был первым, кто отвергал уже в то время возможность создания механического ppm, основанного на использовании сил тяжести. Его позиция отражала более общую тенденцию. Пока изобретатели механических ppm ломали головы над очередными вариантами своих машин, постепенно развивалась механика (и не без их помощи — оттачивала свои положения в дискуссиях с ними). Она вырабатывала новые представления, которые шли дальше античной механики и позволяли количественно точно определить результат одновременного действия на тело нескольких сил. Тем самым новая наука подрывала «под корень» идейную базу механических ppm. Действительно, если выработано четкое правило, как подсчитать результат действия сил, прилагаемых к колесу (или колесам) ppm, то всегда легко определить, будет колесо в равновесии или нет. В первом случае двигатель работать не сможет. Если же, напротив, будет доказано, что неравновесие будет существовать постоянно, то ppm «может жить». Дело, таким образом, сводилось к установлению соответствующего закона механики (точнее, ее раздела — статики).
Первый шаг в этом направлении сделал, по-видимому, великий Леонардо да Винчи (1452-1519 гг.). В рукописи 1515 г. он ввел понятие, которое теперь называется в механике «статическим моментом силы». Со времен Архимеда был известен закон, который определял условия равновесия прямого рычага. Он составлял содержание VI теоремы Архимеда из сочинения по механике: «Два соизмеримых груза находятся в равновесии, если они обратно пропорциональны плечам, на которые эти грузы подвешены». Другими словами (рис. 1.9, а), если силу тяжести (т. е. силу, с которой грузы притягиваются к земле) изобразить в виде отрезков А и В соответствующих направлений и длины, то условие равновесия будет таким: А: В = Ob: Оа , или, что то же самое (следует из свойств пропорции), А ∙ Оа = В ∙ Ob.
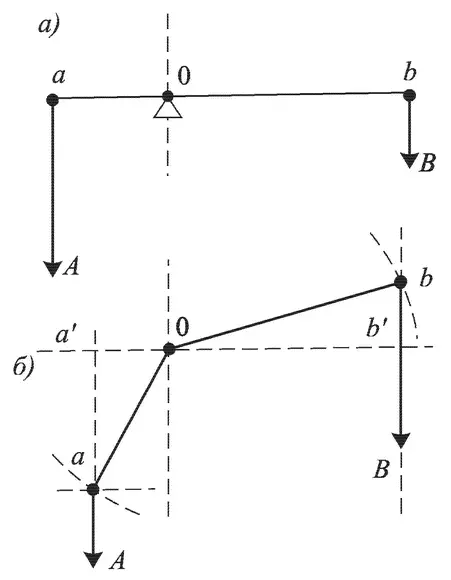
Рис. 1.9. Схема, иллюстрирующая развитие Леонардо да Винчи VI теоремы Архимеда: а — прямой рычаг; б — ломаный рычаг
Таким образом, условие равновесия рычага может быть выражено и так: «Произведения веса каждого груза на длину того плеча рычага, на котором он подвешен, должны быть равны».
При всей его важности закон рычага Архимеда не мог быть использован для анализа равновесия любого колеса механического ppm, работающего с твердыми или жидкими грузами. Дело в том, что для такого анализа нужно было уметь определять равновесие и для случая, когда сила веса груза направлена не под прямым углом к рычагу, как у Архимеда, а под любым углом — острым или тупым. Действительно, стоит посмотреть на рис. 1.3 или 1.6, чтобы увидеть, что сила тяжести направлена под самыми разными углами к соответствующим радиусам колеса. Выделим для примера два груза: один (В) расположен выше оси колеса, а другой (А) ниже (рис. 1.9, б). Как решить задачу в этом, более общем случае?
Леонардо нашел такое решение, он показал его на двух примерах (соответствующие рисунки из его рукописи показаны на рис. 1.10). Относящийся к левому рисунку текст предельно ясен: «Пусть AT — рычаг, вращающийся вокруг точки А. Груз О подвешен в точке Т. Сила А уравновешивает груз О. Проведем линии: АВ перпендикулярно ВО и АС перпендикулярно СТ. Я называю AT действительным рычагом, АВ и АС — «потенциальным рычагом». Существует пропорция N: О = АВ: АС».
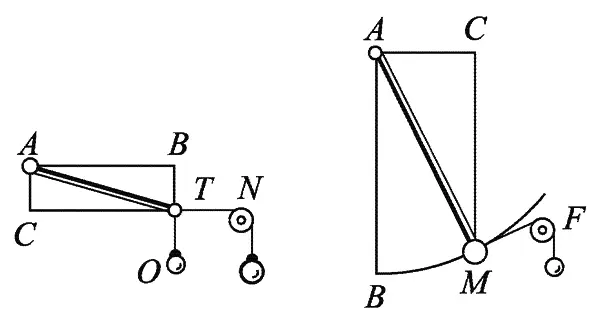
Рис. 1.10. Рисунки Леонардо да Винчи, относящиеся к равновесию рычага
Очевидно, что это соотношение может быть переписано так: О ∙ АВ = N ∙ АС. Другими словами, для равновесия ломаного рычага нужно, чтобы произведения сил на соответствующие «потенциальные рычаги» были равны. Эти «потенциальные рычаги» есть не что иное, как проекции рычага AT на соответствующие оси, перпендикулярные направлению сил, т.е., говоря посовременному, на «плечо силы». Условие равновесия состоит в равенстве статических моментов сил, т.е. произведений сил на проекции плечей рычага на оси, перпендикулярные направлению этих сил.
Читать дальше












