Аналогичное соотношение было выведено Леонардо для случая, показанного на правом рисунке. Здесь F: М = АС: AM. Из него тоже вытекает равенство моментов сил: F ∙ AM = М ∙ АС.
Вернемся к примеру, показанному на рис. 1.9, б. Пользуясь условием Леонардо, получаем, что равновесие наступит при соблюдении равенства А ∙ а’O = В ∙ b’О. Для проверки возможностей любого механического ppm нужно сложить все моменты сил (грузов), расположенных справа от оси О, и то же проделать с грузами, расположенными слева. Первые стремятся повернуть колесо по часовой стрелке, вторые — против. Если общая сумма моментов будет равна нулю (так как их знаки противоположны), то колесо не двинется — наступит равновесие.
Таким путем легко показать, что несмотря на все ухищрения, сумма моментов сил у всех механических ppm равна нулю. Леонардо понимал это очень четко. Стоит только вспомнить слова из одной его записи по поводу ppm: «Искатели вечного движения, какое количество пустейших замыслов пустили вы в мир!»
К сожалению, записи Леонардо остались неизвестными ни его современникам, ни ближайшим потомкам. Только с конца XVIII в. началась планомерная расшифровка его тетрадей.
Задачу создания теории, позволяющей научно подойти к анализу механических ppm и ответить на вопрос об их работоспособности, решил англичанин Джон Уилкинс, епископ Честерский (1599-1658 гг.). Его работа была вполне самостоятельна, поскольку ему не были известны результаты Леонардо, полученные более чем на столетие раньше.
Уилкинс опубликовал свою теорию в книге «Математическая магия», вышедшей в 1648 г. на английском (а не на латинском!) языке. В ней совершенно четко говорится о статическом моменте силы — одном из основополагающих понятий статики.
Изобретатели механических ppm с грузами, основываясь на известном архимедовом законе рычага, полагали, что чем дальше от центра колеса находится груз, тем он сильнее должен поворачивать колесо. Это правило действительно верно, но только для горизонтального рычага (именно его рассматривал Архимед). Распространять его на все грузы, независимо от их расположения на окружности колеса, неверно. Уилкинс наглядно это показал. Ход его мыслей легко проследить с помощью рис. 1.11, на котором изображена схема колеса с центром в точке А. Горизонтальный диаметр DC колеса разделен на 10 равных частей, и через соответствующие точки проведены концентрические окружности с центром в точке А. В разных точках окружностей расположены одинаковые по весу грузы, характер движения которых надо определить. Если грузы расположены на горизонтальном диаметре, задача решается просто — на основе правила Архимеда. Например, груз в 1 фунт в точке С уравновесит 5 фунтов в В, поскольку плечо АС в 5 раз длиннее плеча А В. Уилкинс отмечает, что это соотношение останется в силе, даже если груз будет в точке Е или F, лишь бы они были на той же вертикали, что и С. Другая ситуация возникнет, когда грузы будут находиться не на горизонтальном диаметре, а выше или ниже его, как, например, грузы G, Н или I, К. Уилкинс правильно понял, что в этом случае сила, с которой они будут стремиться вращать колесо в соответствующую сторону, будет другой. Очевидно, что грузы I, К вообще в этом отношении бесполезны, а грузы G и Н потеряют часть своей силы. Чтобы определить действие каждого из них, нужно умножить его вес на длину того отрезка горизонтального диаметра, который находится между точкой А и вертикальной линией, проходящей через точку привеса груза. Для грузов G или Н это будет точка М.
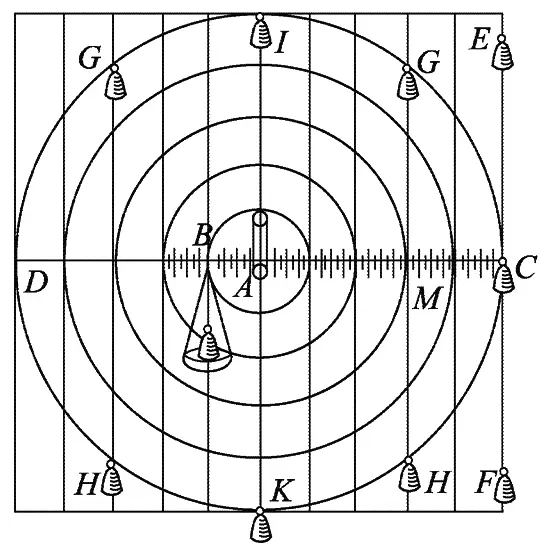
Рис. 1.11. Схема Уилкинса для вывода закона равновесия грузов, расположенных на разных расстояниях от центра колеса
Таким образом, Уилкинс показал, что воздействие груза, вращающего колесо, определяется произведением силы (в данном случае — веса груза) на плечо (в данном случае — отрезок горизонтального радиуса до пересечения с вертикалью, проходящей через центр груза). Равенство всех таких произведений — моментов сил, действующих на колесо, обусловит его равновесие; неравенство — постоянное вращение. Остается только показать, что в любом из механических ppm такое равенство всегда соблюдается, и невозможность их действия доказана.
Читать дальше










