Юрий Дружкин - Очерки теории музыкального моделирования. Книга вторая

Если пропускать пять элементов (с первого на седьмой), то через два шага вернемся к исходному пункту, получив тритон.

Совсем иная картина получится, если двигаться в любом из направлений, пропуская четыре элемента (по квартам), или шесть элементов (по квинтам), что в итоге одно и то же. Ровно через 12 шагов, перебрав по пути все элементы круга, мы возвращаемся к исходному пункту.

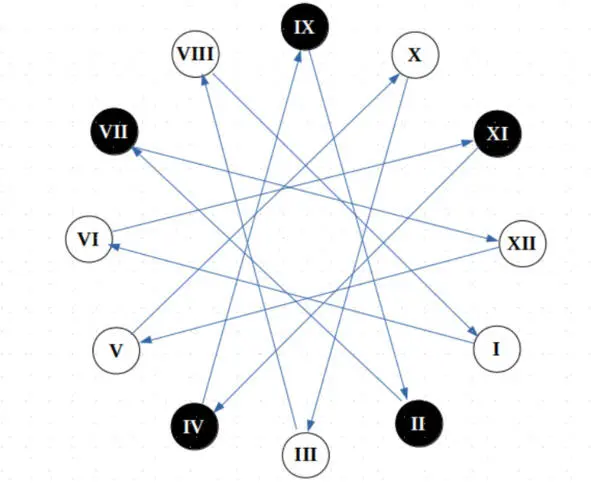
Переход от полутонового круга к квинтовому

В итоге этого путешествия получается квартовый (или квинтовый) круг:

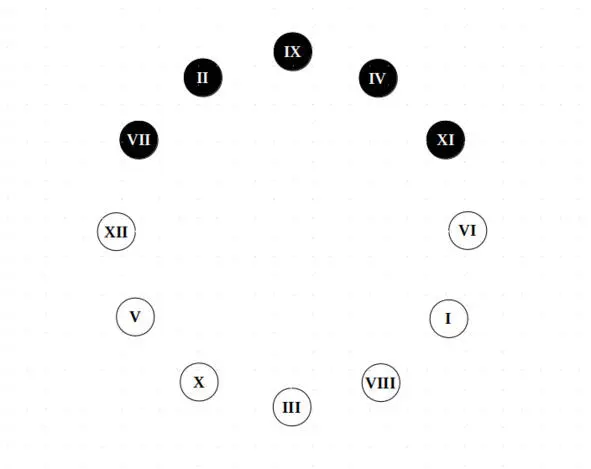
Квинтовый круг

Обратим внимание, что те же самые диаметры играют роль симметрии и антисимметрии, что и в первом случае. Ре-Ля бемоль (Соль диез) – ось симметрии, Фа-Си – ось антисимметрии.

Кроме того (и в этом нетрудно убедиться самостоятельно), если повторить все наши манипуляции, проделанные с полутоновым кругом, по отношению к квинтовому кругу и попробовать двигаться по нему, пропуская сначала один элемент, потом два, потом три, мы опять получим сначала целотонный звукоряд, затем уменьшенный септаккорд, затем увеличенное трезвучие. То есть, обнаруживается высокая степень структурного подобия между полутоновым и квинтовым кругами.

Далее, выполненную для полутонового круга двенадцати-шаговую процедуру можно повторить теперь для квинтового круга. В результате мы вновь получим полутоновый круг. Таким способом они превращаются друг в друга.

Впрочем, это превращение можно осуществить и более простым путем. Надо из шести диаметров нашего круга выбрать либо все четные, либо все нечетные. А затем элементы, располагающиеся на них поменять местами:

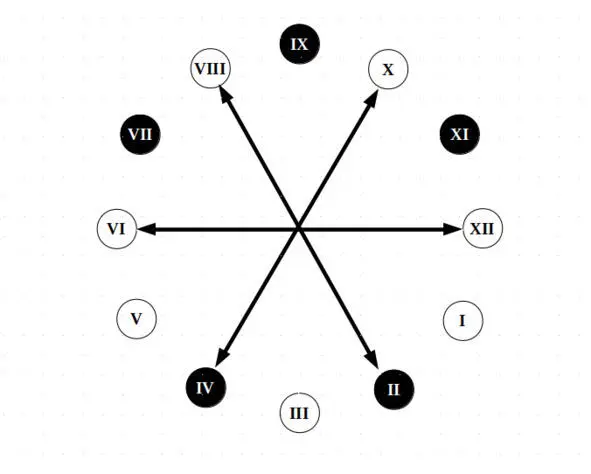
Второй способ перехода

Далее мы можем очень просто «развернуть» этот квинтовый круг в квинтовую прямую, приняв в качестве в качестве идентификационного признака для каждого ее элемента способ порождения данного элемента. Для обозначения этих элементов мы используем привычные названия – до, до диез, ре бемоль и т. д.

После всех проделанных преобразований (манипуляций) система приобрела вид композиции из двух шкал – квинтовой и полутоновой, каждая их который имеет два представления – линейное и круговое. Линейные представления вполне удобно использовать для того, чтобы сделать наглядным характер взаимодействия этих шкал, что мы уже использовали в первом выпуске «Очерков теории музыкального моделирования». Повторим эту схему и в данном тексте:

Квинто-полутоновая схема

На данном шаге нашего исследования мы можем констатировать некоторые важные особенности строения музыкальной моделирующей системы:

– Данная система включает в себя две взаимосвязанные шкалы, упорядочивающие отношения ее элементов – полутоновую и квинтовую.

– Каждая из них имеет два представления:

– линейное – полутоновая прямая и квинтовая прямая

– круговое – полутоновый круг и квинтовый круг.

– Существует преобразование, позволяющее превратить квинтовый круг в полутоновый, а полутоновый в квинтовый. Это преобразование можно выполнить двумя способами. Во-первых, путем движения по кругу. Но не подряд, а шагом по 5 или 7 элементов. Во-вторых, путем взаимного перемещения элементов, находящихся на противоположных концах трех четных либо трех нечетных диаметров.

– Отношение полутоновой и квинтовой шкал характеризуется высоким уровнем симметрии.

– Эта симметрия не означает их смысловой идентичности и взаимозаменяемости. Элементы (кванты) этих шкал – квинта и полутон – существенным образом отличаются по своему звучанию и, как мы знаем из соответствующих разделов первой книги, по своей модельной функции. Полутоновая шкала – пространство. Квинтовая шкала – энергия.

– Полутоновая шкала и все, происходящее на ней, воспринимается непосредственно и достаточно легко. Квинтовая шкала носит значительно более скрытый, латентный, внутренний характер. Изменения, происходящие на ее уровне, воспринимаются, так сказать, на стадии результата. Например, превращение мажорного трезвучия в минорное мы слышим непосредственно, но разность в 7 шагов по квинтовой шкале между мажорной и минорной терцией от нас скрыта.