Юрий Дружкин - Очерки теории музыкального моделирования. Книга вторая

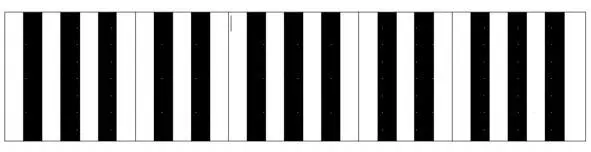
Первое преобразование образа клавиатуры

А теперь сделаем еще один решительный шаг в сторону упрощения (в сторону абстрагирования от непонятных пока делателей) и уберем различия в цвете, сделав все клавиши (все элементы нашей шкалы) белыми:

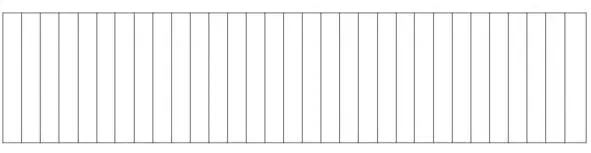
Второе преобразование образа клавиатуры

Ну вот, теперь, когда «все ноты белы», мы не в состоянии «на глаз» определить, где до, где до диез, где ре и т. д. Впрочем, по условию нашего эксперимента, мы пока и не знаем ничего об их существовании.

Представим, что это все же клавиатура какого-то экспериментального музыкального инструмента, настроенного так же, как рояль. Попробуем (оставаясь по условию эксперимента абсолютно музыкально необразованными, хотя и обладающими от природы некоторым музыкальным слухом) подойти к этому инструменты и начать исследовать его свойства, нажимая на клавиши и фиксируя свои слуховые впечатления. Через какое-то время мы заметим, что по мере движения по клавиатуре в одном направлении (например, вправо), мы получаем направленное изменение некоторого различимого слухом качества звука. Изменение постепенное и столь же однонаправленное. Если же начать двигаться в другую сторону, то в обратном же направлении будет меняться и соответствующая характеристика воспринимаемого нами звука. Как мы с вами на самом деле понимаем, речь идет о звуковысотности.

Двигаемся по клавиатуре слева направо – звук становится все выше (тоньше, светлее). Двигаемся справа налево – звук становится все ниже (толще, темнее). Такая упорядоченность, такая направленность клавиатуры нашего экспериментального инструмента позволяет считать эту клавиатуру своего рода материально воплощенной (опредмеченной) шкалой соответствующего параметра. Упорядоченность клавиш в пространства соответствует здесь упорядоченности звуков по «высоте».

Но этим наше исследование не ограничивается. Мы замечаем далее, что изменение параметра происходит не непрерывно, а пошагово, то есть дискретно. Мы, таким образом, имеем дело с дискретной шкалой. Мы по ходу нашей игры еще не знаем, что параметр звуковысотности может изменяться постепенно, не знаем о глиссандо, о вибрации и пр. Мы просто непосредственно наблюдаем, что наша звучащая шкала не дает нам возможности для непрерывного изменения данного параметра.

И еще кое на что мы можем обратить внимание. Хотя, быть может, не сразу. Мы заметим, что разница звучаний двух звуков при нажатии двух соседних клавиш подобна (похожа, одинакова) той разнице, которая соответствует двум другим (в принципе, любым) соседним клавишам. То есть, шкала наша не только дискретна, но и дискретна одинаково, равномерно на всем ее протяжении. Получается что-то подобное тому, как сантиметры на сантиметровой линейке (или дюймы на дюймовой линейке) одинаковы на всем ее протяжении.

Если мы будем экспериментировать с нашей материализованной шкалой и дальше, то с большой вероятностью заметим, что упорядоченность всех ее элементов рождает не только отношение двух противоположных направлений постепенного изменения некоторого существенного звукового параметра, но и отношение «быть между». То есть, если, двигаясь в одном направлении, мы пропустим какой-либо звук, то это пропущенный звук будет находиться между тем, который был взять до него, и тем, который был взят после.

Все это вместе взятое позволяет сделать вывод, что отношение, которое предъявляет нашему восприятию (сознанию) звуковой параметр, соответствующей рассматриваемой шкале, представляет собой отношение порядка. Отношение, весьма похожее на пространственное отношение, в котором находятся окружающие нас предметы. Существенное отличие от физического пространства, в котором мы живем, заключается в том, что это пространство одномерно .

И в этом месте мы останавливаем наш мысленный эксперимент для того, чтобы проанализировать его, пусть и скромные, результаты.

Клавиатура – особая, представленная в материальной форме шкала, предъявляющая нам параметр звуковысотности в его дискретной форме. Но сама идея дискретности неразрывно связана с идеей непрерывности, континуальности. Дискретный шаг означает пропуск некоторого диапазона непрерывных изменений. Наиболее наглядный пример – пунктирная линия. За множеством организованных, выстроенных в едином направлении коротких черточек (пунктира) как бы прячется непрерывная линия. Абсолютную дискретность, «изначальную» дискретность представить (вообразить) невозможно. Всегда возникает вопрос о том, что там находится, между ближайшими точками дискретной шкалы. И тогда получается, что дискретная звуковысотная шкала, материализованная в форме клавиатуры, неразрывно связана с потенциальной континуальной шкалой. Последняя как бы скрывается в тени первой.