Вадим Цудикман - Опционы - Разработка, оптимизация и тестирование торговых стратегий

До сих пор мы рассматривали два подхода к оптимизации – полный перебор, требующий вычисления целевой функции во всех узлах оптимизационного пространства, и целенаправленный поиск. Возможен еще один подход, состоящий в вычислении целевой функции в случайно выбранных узлах оптимизационного пространства. Безусловно, случайный поиск представляет собой самый простой способ оптимизации. Для его реализации достаточно выбрать случайным образом заданное количество узлов и рассчитать значения целевой функции для каждого из них. После этого узел с наибольшим значением выбирается в качестве оптимального решения. Этот метод настолько примитивен, что зачастую вообще не рассматривается в качестве приемлемой методики. Тем не менее во многих случаях (и по многим показателям) случайный поиск может дать достаточно эффективные результаты, не уступающие методам целенаправленного поиска.

Основной и единственный фактор, влияющий на эффективность случайного поиска, – это количество выбираемых ячеек. Чем больше делается попыток, тем выше вероятность того, что оптимальное решение совпадет с глобальным максимумом или будет лежать в непосредственной близости от него. При этом количество попыток должно определяться в зависимости от размеров оптимизационного пространства. В наших примерах это пространство состоит из 3600 ячеек. Если для случайного поиска в таком пространстве использовать 100 попыток, то обследованными окажутся менее 3 % ячеек, что, очевидно, недостаточно для нахождения удовлетворительного оптимального решения. Однако если оптимизационное пространство состоит из 500 ячеек, то 100 попыток составят 20 %, что может оказаться достаточным.

В этом разделе мы проанализируем три аспекта эффективности случайного поиска:

1. Зависимость эффективности поиска от количества случайно выбираемых узлов. Эффективность будет тестироваться для 100, 200, …, 1000 попыток (всего 10 вариантов количества выбираемых узлов).

2. Влияние формы оптимизационного пространства на эффективность случайного поиска. Как и в предыдущем разделе, мы применим метод случайного поиска к оптимизационным пространствам, соответствующим целевым функциям «прибыль» и «процент прибыльных сделок».

3. Сравнение эффективности случайного поиска с двумя методами целенаправленного поиска – покоординатным спуском и методом Хука−Дживса (которые оказались наиболее эффективными среди других методов целенаправленного поиска).

Для анализа эффективности случайного поиска воспользуемся теми же показателями, которые использовались для сравнения четырех методов целенаправленного поиска (таблица 2.7.1).

Как и следовало ожидать, значения всех показателей растут по мере увеличения количества случайно выбранных узлов (рис. 2.7.5 и 2.7.6). Однако темпы этого роста зависят от каждого конкретного показателя. Более того, форма зависимости эффективности поиска от количества попыток различна для разных показателей. Процент оптимальных решений, совпадающих с глобальным максимумом, увеличивается линейно с ростом количества проверенных узлов. С другой стороны, процент оптимальных решений, расположенных в оптимальной области, и среднее значение целевой функции всех оптимальных решений растут нелинейно по мере увеличения количества попыток: в начале рост происходит быстрыми темпами, затем дальнейшее увеличение числа попыток приводит лишь к незначительному росту эффективности поиска.

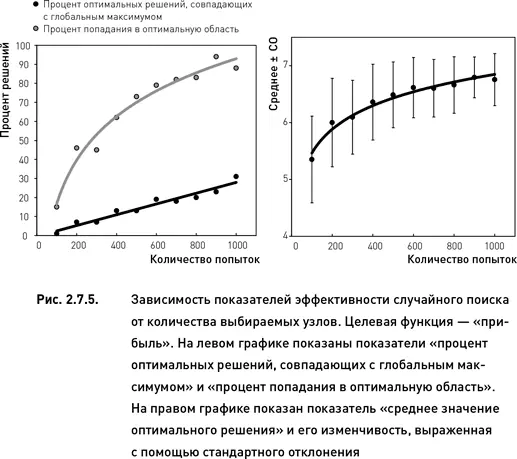
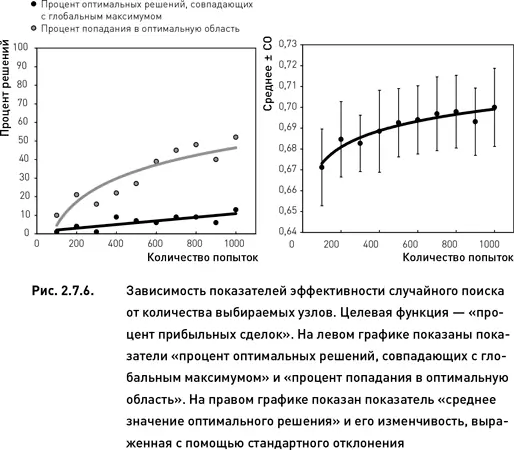
Эффективность случайного поиска выше для оптимизационного пространства, соответствующего целевой функции «прибыль» по сравнению с пространством «процент прибыльных сделок» (сравни левые графики рис. 2.7.5 и 2.7.6). Это полностью совпадает с результатами целенаправленного поиска, полученными в предыдущем разделе. Кроме того, для целевой функции «прибыль» изменчивость показателя «среднее значение оптимального решения» уменьшается при увеличении числа попыток (правый график рис. 2.7.5). В то же время для целевой функции «процент прибыльных торговых циклов» такая зависимость не наблюдается (правый график рис. 2.7.6).

По показателю «процент оптимальных решений, совпадающих с глобальным максимумом» случайный поиск уступает покоординатному подъему и методу Хука−Дживса. Однако при использовании достаточного количества попыток случайный поиск оказывается более эффективным по двум другим показателям. Для целевой функции «прибыль» случайный поиск становится эффективнее покоординатного подъема по показателям «среднее значение оптимального решения» и «процент попадания в оптимальную область» начиная с 400 попыток. При использовании 500 попыток данный метод превосходит и вторую методику, Хука−Дживса (сравни рис. 2.7.5 с данными таблицы 2.7.1). Для целевой функции «процент прибыльных сделок» случайный поиск становится эффективнее покоординатного подъема и метода Хука−Дживса по проценту попаданий в оптимальную область начиная с 600 попыток. По среднему значению оптимального решения случайный поиск превосходит эти две методики начиная с 700 попыток (сравни рис. 2.7.6 с данными таблицы 1).