Феликс Филатов - Клеймо создателя

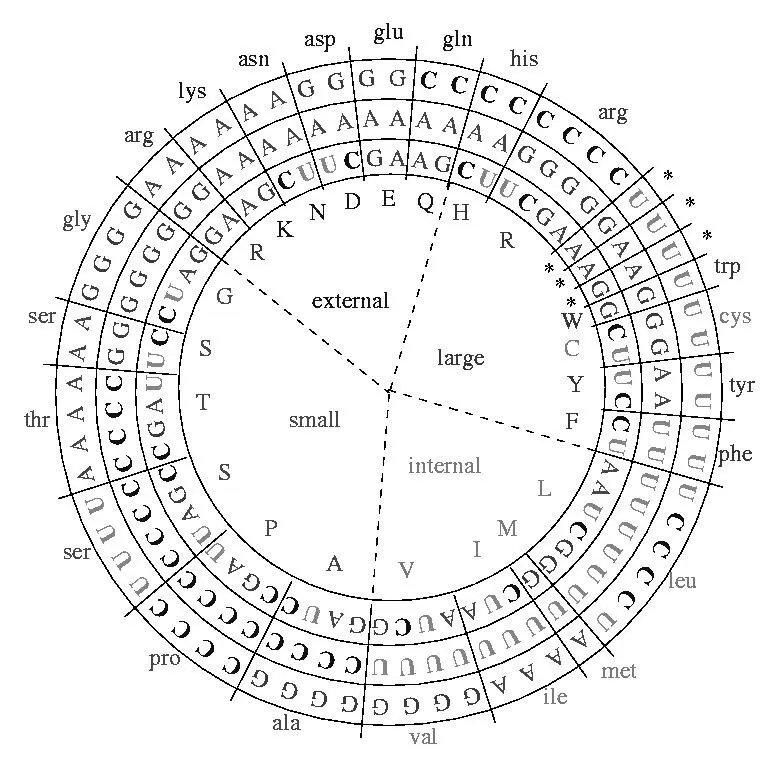
Как мы упоминали, симметрия описанного представления генетического кода имеет место не только по молекулярной массе аминокислот, но и по другим их параметрам (строки 11—15). Замена в третьей позиции пары симметричных кодонов пурина пиримидином – и наоборот – в определенной мере сохраняет, например, гидрофобность кодируемых продуктов, хотя размер аминокислоты при этом, конечно, основательно меняется. Однако, ни гидрофобность, ни еще одна характеристика – PR (строка 15) – которую Карл Вѐзе и его группа описали, как основу регулярности генетического кода и соответствия кодонов и продуктов кодирования, не могут сравниться по строгости симметрий с молекулярной массой аминокислот, что хорошо демонстрирует приведенная таблица Владимира Щербака. Неканонические ключи кодирования (строка 17) тоже выглядят в этих таблицах довольно беспорядочными и случайными отклонениями.

За весь этот рисунок кооперативной симметрии генетического кода , на основе молекулярных масс его компонентов, за ее красоту и гармонию, не имеющую к тому же сколько-нибудь внятного физического, химического или молекулярно-биологического обоснования, мой друг назвал описанную таблицу каллиграммой ( красивой записью ). Термин этот принадлежит Гийому Апполинеру, который – в экспериментальном порядке попытался организовать некоторые свои тексты так, чтобы продемонстрировать их симметрию. Их он и называл calligrammes .

В следующей главе мы покажем, что симметрии каллиграммы Щербака имеют неожиданный количественный характер, то есть, по-видимому, даже более сущностны, нежели только что описано. Стоит, однако, отметить, что известные небольшие отклонения от универсального генетического кода могут серьезно нарушать симметрии каллиграммы. Например, генетический код митохондрий позвоночных, который, по одним представлениям, был предшественником универсального, а по другим – сам происходил из него, отличается тем, что у него отсутствуют нечетные группы вырожденности, так что две четные прямо соответствуют двум октетам Румера. При этом дублет TG кодирует цистеин, если в третьей позиции триплета стоит пиримидин, и триптофан, если в третьей позиции – пурин. То же относится и к дублету АТ : AT Y = I, AT R = M. И еще одно отличие от универсального: триплет AG R кодирует не аргинин, а сигналы терминации (0). Это означает, что описанная каллиграмма Щербака, сама по себе, как будто, не является обязательным условием организации генетического кодирования (земных?) организмов. Вместе с тем, Андрей Хренников и Сергей Козырев 56, используя так называемые р -адические числа, показали наличие значительной регулярности и в этой версии генетического кода. Автор не берется комментировать их работу, поскольку ровно ничего не понимает в р -адических числах и в d -адических плоскостях. Однако, она каким-то образом связывает регулярную организацию (в том числе и симметрии) генетического кода с его защищенностью. В своих рассуждениях Хренников и Козырев отталкивались от представления кодирующих триплетов, предложенного Роз-Мари Свансон 5757 и позднее уточненного Драганом Босняцким 5858 с соавторами на основе подхода, используемого для решения хорошо известной Проблемы Путешествующего Продавца (ППП). В этом представлении последовательность кодирующих триплетов образует цикл, известный как « код Грея »:

Напомню, что кодом Грея называется любая циклическая последовательность всех наборов из нулей и единиц, в которой два соседних набора отличаются только по одной компоненте (дельта Хемминга). Другими словами, код Грея – это система замкнутой организации числового ряда, в которой два соседних значения различаются только в одном разряде. Вот как выглядит 3-битный двоичный код Грея (каждое трехзначное число представлено здесь вертикально; то есть чтение его сверху вниз соответствует обычному чтению слева направо) в линейном представлении:

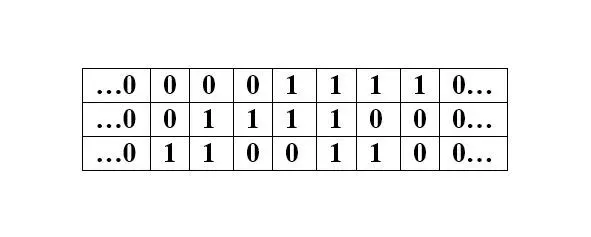
Первое и последнее числа ( 000) совпадают, указывая на замкнутость ряда. Читателю предлагается обратить внимание на то, что числа кода Грея (двоичные в данном случае) расположены в последовательности, не совпадающей с натуральным рядом: преобразованные в десятичные, они дают здесь последовательность 0— 1— 3— 2— 6— 7— 5— 4— 0.