Если без проведения сокращений численность сотрудников не имеет устойчивого равновесия, то может ли принудительное сокращение привести к стабильности? Имеет ли это экономический смысл?
Используйте программу longterm.m для создания диаграмм, показывающих изменения моделируемой численности в долгосрочной перспективе по мере изменения параметров модели.
% longterm.m
fun = @(x,r) x + r*x*(1-x);
x0 = .99; a0 = 0; a1 = 3; N = 777; preL = 200; L = 100;
mat = bifur(fun,x0,a0,a1,N,preL,L);
function mat = bifur(fun,x0,a0,a1,N,preL,L,p_siz)
% –
% Функция bifur: строит однопараметрическую диаграмму бифуркаций
% Вход: fun = некоторая функция @(x,para)
% x0 = стартовое значение для x
% a0 = начальное значение параметра a
% a1 = конечное значение параметра a
% N = количество интервалов для параметра 'a' на отрезке [a0;a1]
% preL = количество предварительно пропускаемых итераций для
% преодоления переходного процесса перед стабилизацией
% L = количество итераций для каждой начальной пары
% от (x0,параметр a)
% p_siz = размер маркера, по умолчанию 1
% Выход: mat = бифукационная матрица размера N на L
% которая хранит последовательность длины L
% для каждой пары (x0, параметр a)
% –
% установки по умолчанию
if ~exist('p_siz','var')
p_siz = 1;
end
% инициализация
mat = zeros(N,L);
a = linspace(a0,a1,N);
% основной цикл
format long
for i = 1:N
ca = a(i); % выбрать одно значение параметра в каждый момент времени
for j = 1:L % сгенерировать последовательность длиной L
if j == 1
pre = x0; % инициализируем стартовое значение
for k = 1:preL % пропускаем значения переходного процесса
nxt = fun(pre,ca);
pre = nxt;
end
end
nxt = fun(pre,ca); % вычисляем следующее значение последовательности
mat(i,j) = nxt; % сохраняем в результирующей матрице mat
pre = nxt; % последнее значение будет начальным для следующей итерации
end
end
% построение графика
dcolor = [0,0,1]; % настройка цвета маркера: синий
[r,c] = meshgrid(1:L,a); % наполяем сетку данных координат
surf(r,c,mat,'Marker','*','MarkerSize',p_siz,'FaceColor','None','MarkerEdgeColor', dcolor,'EdgeColor','None')
view([90,0,0]) % фиксируем направление камеры
ylim([a0,a1]) % размещаем данные на диаграмме
end
2. Для популяции со временем регенерации значительно меньшей единицы времени может быть неуместно думать о пропускной способности как о константе. Исследуйте, что произойдет, если пропускная способность изменяется синусоидально. Для начала попробуйте понять следующие команды MATLAB:
t=[0:50]
K=5+sin((2*pi/12)*t)
p=.1; pops=p
for i=1:50
p=p+.2*p*(1-p/K(i));
pops=[pops p];
end
plot(t,K,t,pops)
Рекомендации
Объясните, почему синусоидально изменяющаяся пропускная способность может иметь физический или социально-экономический смысл при некоторых обстоятельствах.
Исследуйте поведение модели для различных вариантов 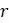 и
и 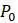 . Колеблется ли
. Колеблется ли 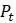 вместе с
вместе с 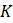 ? Обратите особое внимание на то, когда популяция достигает пика и каково среднее значение
? Обратите особое внимание на то, когда популяция достигает пика и каково среднее значение 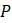 в долгосрочной перспективе. Соответствуют ли результаты машинных экспериментов вашей интуиции?
в долгосрочной перспективе. Соответствуют ли результаты машинных экспериментов вашей интуиции?
Что происходит, если изменяется частота колебаний пропускной способности? Попробуйте заменить 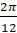 в предыдущем примере на
в предыдущем примере на 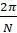 при разных N.
при разных N.
По мере увеличения 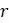 эта модель демонстрирует бифуркации? Хаос?
эта модель демонстрирует бифуркации? Хаос?
3. Изучите, что произойдет, если пропускная способность изменяется случайным образом в логистической модели, и, в частности, влияние такой пропускная способность на небольшие популяции. Нужно будет знать, что команда rand(1) в MATLAB выдает случайное число в диапазоне от 0 до 1 с равномерным распределением, и что randn(1) генерирует случайное число из нормального распределения с матожиданием 0 и стандартным отклонением 1. Можете начать с использования программы onepop.m с выражением типа 10 + rand(1) в качестве пропускной способности в логистической модели.
Рекомендации
Возможно, 10*rand(1) или 10+2*randn(1) были бы лучшей формулой для значений 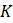 в экспериментальной модели. Опишите качественные различия между реальными ситуациями, которые могут описывать эти математические выражения.
в экспериментальной модели. Опишите качественные различия между реальными ситуациями, которые могут описывать эти математические выражения.
Для выбранного выражения изучите поведение модели для различных вариантов 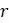 и
и 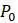 . Как ведет себя
. Как ведет себя 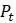 ? Каково среднее значение
? Каково среднее значение 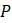 в долгосрочной перспективе? Соответствуют ли результаты вашей математической интуиции?
в долгосрочной перспективе? Соответствуют ли результаты вашей математической интуиции?
Читать дальше

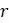 и
и 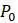 . Колеблется ли
. Колеблется ли 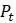 вместе с
вместе с 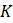 ? Обратите особое внимание на то, когда популяция достигает пика и каково среднее значение
? Обратите особое внимание на то, когда популяция достигает пика и каково среднее значение 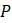 в долгосрочной перспективе. Соответствуют ли результаты машинных экспериментов вашей интуиции?
в долгосрочной перспективе. Соответствуют ли результаты машинных экспериментов вашей интуиции?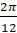 в предыдущем примере на
в предыдущем примере на 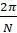 при разных N.
при разных N.










