Случай 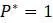 гораздо интереснее. Во-первых, когда
гораздо интереснее. Во-первых, когда 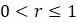 , что равносильно
, что равносильно 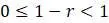 , модель имеет стабильное равновесие в точке
, модель имеет стабильное равновесие в точке 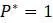 . Формула
. Формула 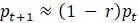 показывает, что знак
показывает, что знак 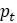 при этом никогда не изменится; хотя отклонение уменьшается, первоначально положительное отклонение остается положительным, а изначально отрицательное – отрицательным. Популяция просто движется к равновесию, никогда не превышая его.
при этом никогда не изменится; хотя отклонение уменьшается, первоначально положительное отклонение остается положительным, а изначально отрицательное – отрицательным. Популяция просто движется к равновесию, никогда не превышая его.
Далее, когда 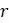 увеличивается настолько, что
увеличивается настолько, что 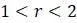 , то
, то 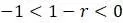 и равновесие будет все еще стабильным. Однако, теперь видим, что так как
и равновесие будет все еще стабильным. Однако, теперь видим, что так как 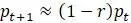 , то знак
, то знак 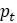 будет чередоваться между положительным и отрицательным значением по мере увеличения
будет чередоваться между положительным и отрицательным значением по мере увеличения 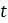 . Таким образом, можно видеть колебательное поведение выше и ниже точки равновесия, поскольку отклонение от равновесного значения имеет чередование знака. Таким образом, популяция приближается к равновесию как затухающее колебание.
. Таким образом, можно видеть колебательное поведение выше и ниже точки равновесия, поскольку отклонение от равновесного значения имеет чередование знака. Таким образом, популяция приближается к равновесию как затухающее колебание.
Подумаем о том, почему такое колебание может произойти с точки зрения моделируемой популяции. Если 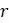 , мера скорости воспроизводства новых ленов популяции, достаточно велика, то популяция ниже пропускной способности окружающей среды может за один временной шаг своего развития временно вырасти настолько, что превысит пропускную способность. Как только численность превышает пропускную способность, популяция вымирает достаточно быстро, чтобы к следующему шагу она снова оказалась ниже пропускной способности окружающей среды. Но затем её численность снова вырастет настолько, чтобы превзойти критическое значение. Как будто популяция перенастраивается и адаптируется заново на каждом временном интервале.
, мера скорости воспроизводства новых ленов популяции, достаточно велика, то популяция ниже пропускной способности окружающей среды может за один временной шаг своего развития временно вырасти настолько, что превысит пропускную способность. Как только численность превышает пропускную способность, популяция вымирает достаточно быстро, чтобы к следующему шагу она снова оказалась ниже пропускной способности окружающей среды. Но затем её численность снова вырастет настолько, чтобы превзойти критическое значение. Как будто популяция перенастраивается и адаптируется заново на каждом временном интервале.
Если параметр 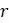 логистической модели окажется больше только что рассмотренных значений, то популяция не приблизится к равновесию. Когда
логистической модели окажется больше только что рассмотренных значений, то популяция не приблизится к равновесию. Когда 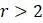 , получится
, получится 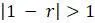 и поэтому ранее устойчивое равновесие
и поэтому ранее устойчивое равновесие 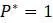 становится неустойчивым. Таким образом, происходит резкое качественное изменение поведения численности популяции по мере дальнейшего увеличения параметра
становится неустойчивым. Таким образом, происходит резкое качественное изменение поведения численности популяции по мере дальнейшего увеличения параметра 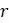 . Отсюда возникает интересный вопрос, каковы возможности модели с двумя неустойчивыми равновесиями и без устойчивых. Какое поведение тогда можно ожидать в долгосрочной перспективе?
. Отсюда возникает интересный вопрос, каковы возможности модели с двумя неустойчивыми равновесиями и без устойчивых. Какое поведение тогда можно ожидать в долгосрочной перспективе?
Компьютерный эксперимент показывает, что для значений 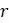 чуть больше 2 популяция попадает в 2-цикл, её численность бесконечно прыгает взад и вперед между значением выше 1 и значением ниже 1. По мере дальнейшего увеличения
чуть больше 2 популяция попадает в 2-цикл, её численность бесконечно прыгает взад и вперед между значением выше 1 и значением ниже 1. По мере дальнейшего увеличения 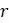 значения в 2-цикле меняются, но наличие 2-цикла сохраняется до тех пор, пока не достигнем другого значения
значения в 2-цикле меняются, но наличие 2-цикла сохраняется до тех пор, пока не достигнем другого значения 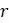 , при котором происходит еще одно внезапное качественное изменение. На этот раз видим, что 2-цикл становится 4-циклом. Дальнейшее увеличение
, при котором происходит еще одно внезапное качественное изменение. На этот раз видим, что 2-цикл становится 4-циклом. Дальнейшее увеличение 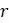 производит 8-циклы, затем 16-циклы и так далее.
производит 8-циклы, затем 16-циклы и так далее.
Читать дальше

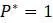 гораздо интереснее. Во-первых, когда
гораздо интереснее. Во-первых, когда 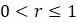 , что равносильно
, что равносильно 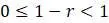 , модель имеет стабильное равновесие в точке
, модель имеет стабильное равновесие в точке 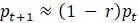 показывает, что знак
показывает, что знак 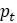 при этом никогда не изменится; хотя отклонение уменьшается, первоначально положительное отклонение остается положительным, а изначально отрицательное – отрицательным. Популяция просто движется к равновесию, никогда не превышая его.
при этом никогда не изменится; хотя отклонение уменьшается, первоначально положительное отклонение остается положительным, а изначально отрицательное – отрицательным. Популяция просто движется к равновесию, никогда не превышая его.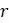 увеличивается настолько, что
увеличивается настолько, что 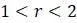 , то
, то 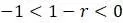 и равновесие будет все еще стабильным. Однако, теперь видим, что так как
и равновесие будет все еще стабильным. Однако, теперь видим, что так как 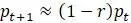 , то знак
, то знак 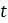 . Таким образом, можно видеть колебательное поведение выше и ниже точки равновесия, поскольку отклонение от равновесного значения имеет чередование знака. Таким образом, популяция приближается к равновесию как затухающее колебание.
. Таким образом, можно видеть колебательное поведение выше и ниже точки равновесия, поскольку отклонение от равновесного значения имеет чередование знака. Таким образом, популяция приближается к равновесию как затухающее колебание.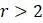 , получится
, получится 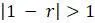 и поэтому ранее устойчивое равновесие
и поэтому ранее устойчивое равновесие 










